题目内容
对于任意两个正整数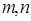 ,定义某种运算“※”如下:当
,定义某种运算“※”如下:当 都为正偶数或正奇数时,
都为正偶数或正奇数时,  ※
※ =
= ;当
;当 中一个为正偶数,另一个为正奇数时,
中一个为正偶数,另一个为正奇数时,  ※
※ =
= .则在此定义下,集合
.则在此定义下,集合 ※
※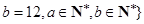 中的元素个数是( )
中的元素个数是( )
| A.10个 | B.15个 | C.16个 | D.18个 |
B
解析试题分析:由于两个正整数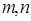 ,定义某种运算“※”如下:当
,定义某种运算“※”如下:当 都为正偶数或正奇数时,
都为正偶数或正奇数时,  ※
※ =
= ;当
;当 中一个为正偶数,另一个为正奇数时,
中一个为正偶数,另一个为正奇数时,  ※
※ =
= 所以
所以 ※
※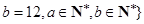 中当
中当 都为偶数时有(2,10),(10,2),(4,8),(8,4),(6,6)共5个元素;当
都为偶数时有(2,10),(10,2),(4,8),(8,4),(6,6)共5个元素;当 都是奇数时有(1,11),(11,1),(3,9),(9,3),(5,7),(7,5);共有6个元素;当
都是奇数时有(1,11),(11,1),(3,9),(9,3),(5,7),(7,5);共有6个元素;当 为一奇一偶时有(1,12),(12,1),(3,4),(4,3).综上共有15个元素.
为一奇一偶时有(1,12),(12,1),(3,4),(4,3).综上共有15个元素.
考点:1.新定义的问题.2.因数分解.3.集合的含义.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
| |||||||||||||||
设集合 ,
, ,则有( )
,则有( )
A. | B. | C. | D. |
已知集合 ,若对于任意
,若对于任意 ,存在
,存在 ,使得
,使得 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
① ; ②
; ② ;
;
③ ; ④
; ④ .
.
其中是“垂直对点集”的序号是( )
| A.①② | B.②③ | C.①④ | D.②④ |
已知集合 =( )
=( )
A. | B. |
C. | D. |
若集合 ,
, ,
, ,则满足条件的实数
,则满足条件的实数 的个数有( )
的个数有( )
| A.1 | B.2 | C.3 | D.4 |
若集合 则“
则“ ”是“
”是“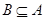 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合 ,则
,则
A. | B. | C. | D. |
 M)∩N=( )
M)∩N=( )


