Question

设a∈R，讨论关于x的方程x³+3x²-a=0的相异实根的个数？

Answer 1

分析：设方程左边对应三次多项式函数f（x），利用导数工具研究函数的单调性，可得f（x）的极大值是f（-2）=4-a，极小值是f（0）=a．由此结合函数的图象观察，进行分类讨论即可得到各种情况下原方程的实数根的个数．

解答：解∵设函数f（x）=x³+3x²-a，求导函数得f'（x）=3x²+6x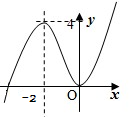
∴f'（x）=0的两根分别为x₁=-2，x₂=0
∵x＜-2或x＞0时，f'（x）＞0；-2＜x＜0时，f'（x）＜0
∴函数f（x）的减区间为（-2，0）；增区间为（-∞，-2）和（0，+∞）
因此，函数f（x）的极大值是f（-2）=4-a，极小值是f（0）=-a
作出函数的草图，如右图所示，可得
（1）当4-a＜0或-a＞0时，即a＜0或a＞4时，函数f（x）的图象与x轴只有一个交点，
可得原方程只有一个根．
（2）当4-a=0或-a=0时，即a=0或a=4时，函数f（x）的图象与x轴有两个交点，即原方程有两个相异实根．
（3）当0＜a＜4时，函数f（x）的图象与x轴有三个交点，原方程有三个相异实根．

点评：本题给出含有字母参数的三次方程，讨论方程根的个数．着重考查了利用导数研究函数的单调属于和三次多项式的极值求法等知识，属于基础题．