Question

有A、B两个黑布袋，A布袋中有四个除标号外完全相同的小球，小球上分别标有数字0，1，2，3，B布袋中有三个除标号外完全相同的小球，小球上分别标有数字0，1，2．小明先从A布袋中随机取出一个小球，用m表取出的球上标有的数字，再从B布袋中随机取出一个小球，用n表示取出的球上标有的数字．若用（m，n）表示小明取球时m与n的对应值，
求关于x的一元二次方程x²-mx+

1

2

n=0有实数根的概率．

Answer 1

分析：依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．

解答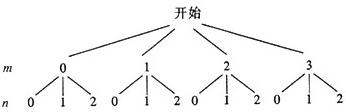：解：∴（m，n）所有取值是（0，0），（0，1），
（0，2），（1，0），（1，1），（1，2），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）．共12个；
由原方程得；△=m²-2n．
当m，n对应值为（0，0），（1，0），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）时，
△≥0，原方程有实数根．
故P（△≥0）=

8

12

=

2

3

．
答：原方程有实数根的概率为

2

3

．

点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．