题目内容
对任意正整数n定义双阶乘n!!如下:当n为偶数时,n!!=n(n-2)(n-4)•…•4•2;当n为奇数时,n!!=n(n-2)(n-4)•…•3•1,现有如下四个命题:
①(2011!!)(2010!!)=2011!;
②2010!!=2×1005!;
③设1010!!=a×10k(a,k∈N*),若a的个位数不是0,则k=112;
④设15!!=
| a | n1 1 |
| a | n2 2 |
| a | nm m |
则其中正确的命题是
分析:先利用题中的新定义判断出①真②假,再根据双阶乘的定义,判断出需要解决的问题,判断出③假④真.
解答:解:由定义,①为真命题;,②为假命题;
由条件就是要求从个位数算起到第1个不是0的数字之间 的尾数中共有多少个连续的0,也即为 中各数的尾数所含0的个数的总和,共有 个,而 还能产生0(如 等)∴③是假命题;,∴④为真命题,
故答案为:①④.
由条件就是要求从个位数算起到第1个不是0的数字之间 的尾数中共有多少个连续的0,也即为 中各数的尾数所含0的个数的总和,共有 个,而 还能产生0(如 等)∴③是假命题;,∴④为真命题,
故答案为:①④.
点评:解决新定义的题目,一定要认真审题,理解透新定义的含义是关键,是近几年常考题型.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
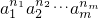 (ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4;
(ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4; (ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4;
(ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4; (ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4;
(ai为正质数,ni为正整数(i=1,2,…,m)),则(ni)max=4;