题目内容
已知函数
,若
成等差数列.
(1)求数列
的通项公式；
(2)设
是不等式
整数解的个数，求；
(3)记数列
的前n项和为
，是否存在正数
，对任意正整数
，使
恒成立？若存在，求的取值范围；若不存在，说明理由.
【答案】
解：（1）由题可知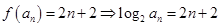
………………（2分）
得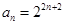
．………………………………………………………………（4分）
（2）原式化简：
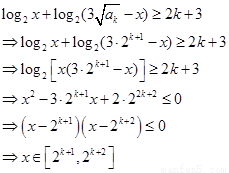……………………………………（8分）
其中整数个数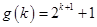
．…………………………………………（10分）
（3）由题意，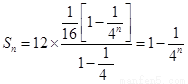
，
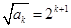…………………（12分）
又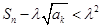
恒成立，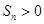
，
，
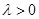所以当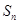
取最大值，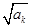
取最小值时，
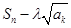取到最大值．……（14分）
又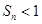
，
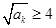，所以
……………………………………（16分）
解得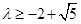
………………………………………………………………（18分）
【解析】略
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
有两个不相等的实根，且必有一个根属于
成等差数例，设函数
的图象的对称轴为
。