题目内容
设α和β为两个不重合的平面，给出下列四个命题：
①若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；②若α外一条直线l与α内的一条直线平行，则l和α平行；③设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；④直线l与α垂直的充分必要条件是l与α内的两条直线垂直．其中为真命题的是________(写出所有真命题的序号)．
①②
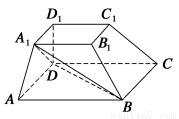
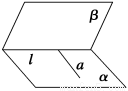
【解析】由①知α内两条相交直线分别平行于平面β，则两条相交直线确定的平面α平行于平面β，故①为真命题；由线面平行的判定定理知，②为真命题；对于③，如图，α∩β＝l，a?α，a⊥l，但不一定有α⊥β，故③为假命题；
对于④，直线l与平面α垂直的充分必要条件是l与α内的两条相交直线垂直，故④为假命题．
综上所述，真命题的序号为①②.
练习册系列答案
相关题目
