��Ŀ����
��һ��Ϊһ�����ڵ���ij��Ʒ�����۸���Ʒ���̵�����ۼ۸�ʱ���֣�����Ʒ�ij����۸�����6Ԫ�����ϰ��·����������߲����ģ���֪3�·ݳ����۸����Ϊ8Ԫ��7�·ݳ����۸����Ϊ4Ԫ��������Ʒ���̵�����ۼ۸�����8Ԫ�����ϰ������������߲����ģ�����֪5�·����ۼ����Ϊ10Ԫ��9�·����ۼ����Ϊ6Ԫ������ij�̵�ÿ�¹���������Ʒm�����ҵ������꣬��ֱ�д������Ʒ�ij����۸��������ۼ۸�����ӯ�������Ľ���ʽ��
���𰸡��������������۸�����Ϊ f��x��=A1sin����1x+��1��+k1��x��[0��12]�����ۼ۸�����Ϊg��x��=A2sin����2x+��2��+k2��x��[0��12]��������֪��A1 A2 ��1 ��2 k1 k2�ֱ�������ٸ���ӯ��=m×�����ۼ۸�-�����۸����ӯ��������
����⣺������۸���Ϊ f��x��=A1sin����1x+��1��+k1��x��[0��12]
���ۼ۸���Ϊg��x��=A2sin����2x+��2��+k2��x��[0��12}
�����裬A1=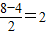 ��k1=6
��k1=6
��1= =
=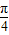 A2=
A2= K2=8��2=
K2=8��2=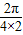 =
=
����3��8������f��x���ɵ� 2sin��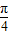 ×3+��1��+6=8 �æ�1=-
×3+��1��+6=8 �æ�1=-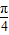 +2k�У�k��Z
+2k��k��Z
����5��10������g��x���ɵ� 2sin�� ×5+��2��+8=10 �æ�2=-
×5+��2��+8=10 �æ�2=-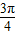 +2k�У�k��Z
+2k��k��Z
�� �����۸���Ϊ f��x��=2sin�� x-
x- ��+6��x��[0��12}
��+6��x��[0��12}
���ۼ۸���Ϊg��x��=2sin��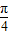 x-
x-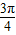 ��+8��x��[0��12}
��+8��x��[0��12}
����ӯ������ΪH��x����H��x��=[g��x��-f��x��]×m=2m[sin��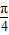 x-
x-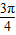 ��-sin��
��-sin�� x-
x- ��+1]x��[0��12}
��+1]x��[0��12}
��ӯ������ΪH��x��=2m[sin�� x-
x-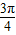 ��-sin��
��-sin�� x-
x-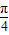 ��+1]x��[0��12}
��+1]x��[0��12}
�����Ʒ�ij����۸���Ϊ f��x��=2sin��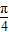 x-
x-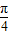 ��+6��x��[0��12}
��+6��x��[0��12}
���ۼ۸���Ϊg��x��=2sin��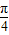 x-
x-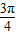 ��+8��x��[0��12}
��+8��x��[0��12}
ӯ������ΪH��x��=2m[sin��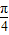 x-
x-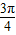 ��-sin��
��-sin�� x-
x-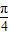 ��+1]x��[0��12}
��+1]x��[0��12}
���������⿼�������Ǻ�����ͼ������ʣ��ر���y=Asin��wx+�գ���ͼ�����ʼ���ʵ�����壬����ʱҪ�����������ϸ���
����⣺������۸���Ϊ f��x��=A1sin����1x+��1��+k1��x��[0��12]
���ۼ۸���Ϊg��x��=A2sin����2x+��2��+k2��x��[0��12}
�����裬A1=
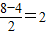 ��k1=6
��k1=6��1=
 =
=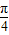 A2=
A2= K2=8��2=
K2=8��2=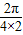 =
=
����3��8������f��x���ɵ� 2sin��
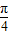 ×3+��1��+6=8 �æ�1=-
×3+��1��+6=8 �æ�1=-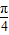 +2k�У�k��Z
+2k�У�k��Z����5��10������g��x���ɵ� 2sin��
 ×5+��2��+8=10 �æ�2=-
×5+��2��+8=10 �æ�2=-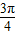 +2k�У�k��Z
+2k�У�k��Z�� �����۸���Ϊ f��x��=2sin��
 x-
x- ��+6��x��[0��12}
��+6��x��[0��12}���ۼ۸���Ϊg��x��=2sin��
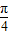 x-
x-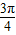 ��+8��x��[0��12}
��+8��x��[0��12}����ӯ������ΪH��x����H��x��=[g��x��-f��x��]×m=2m[sin��
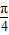 x-
x-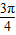 ��-sin��
��-sin�� x-
x- ��+1]x��[0��12}
��+1]x��[0��12}��ӯ������ΪH��x��=2m[sin��
 x-
x-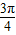 ��-sin��
��-sin�� x-
x-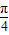 ��+1]x��[0��12}
��+1]x��[0��12}�����Ʒ�ij����۸���Ϊ f��x��=2sin��
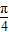 x-
x-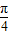 ��+6��x��[0��12}
��+6��x��[0��12}���ۼ۸���Ϊg��x��=2sin��
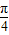 x-
x-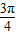 ��+8��x��[0��12}
��+8��x��[0��12}ӯ������ΪH��x��=2m[sin��
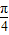 x-
x-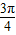 ��-sin��
��-sin�� x-
x-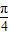 ��+1]x��[0��12}
��+1]x��[0��12}���������⿼�������Ǻ�����ͼ������ʣ��ر���y=Asin��wx+�գ���ͼ�����ʼ���ʵ�����壬����ʱҪ�����������ϸ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ