题目内容
椭圆 与双曲线
与双曲线 有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线
有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线 于M、N两点,且
于M、N两点,且 .
.
(1)求椭圆E的方程;
(2)设P是椭圆E上第一象限内的点,点P关于原点O的对称点为A、关于x轴的对称点为Q,线段PQ与x轴相交于点C,点D为CQ的中点,若直线AD与椭圆E的另一个交点为B,试判断直线PA,PB是否相互垂直?并证明你的结论.
【答案】
(1) 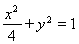 ;(2)
;(2)  .证明见解析.
.证明见解析.
【解析】
试题分析:(1)设点 ,
,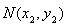
设直线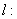
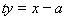 ,代入
,代入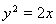 并整理得
并整理得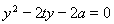
利用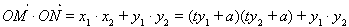
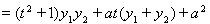
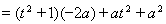
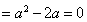 解得
解得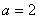 ,再由
,再由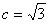 求得
求得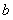 .
.
(2) 首先判断得出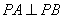 .可通过证明
.可通过证明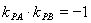 或
或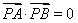 ,达到目的.
,达到目的.
设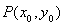 ,得到
,得到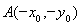 ,
,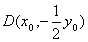 且
且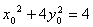
将直线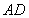 的方程
的方程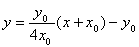 代入椭圆的方程并整理得到
代入椭圆的方程并整理得到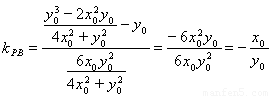 由
由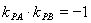 得证.
得证.
试题解析:(1)设点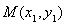 ,
,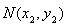
设直线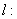
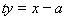 ,代入
,代入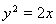 并整理得
并整理得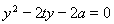
所以 2分
2分
故有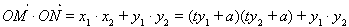
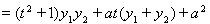
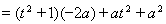
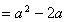 解得
解得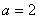 5分
5分
又椭圆与双曲线有公共的焦点,故有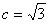
所以椭圆的方程为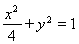 . 7分
. 7分
(2) 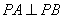
证明:设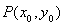 ,则
,则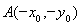 ,
,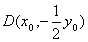 且
且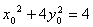
将直线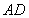 的方程
的方程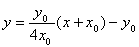 代入椭圆的方程并整理得
代入椭圆的方程并整理得
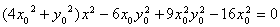 9分
9分
由题意可知此方程必有一根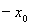
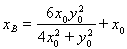 ,
, 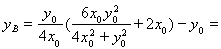
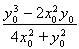
所以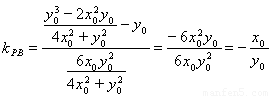 12分
12分
故有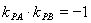 , 即
, 即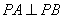 13分
13分
考点:椭圆的标准方程,平面向量的坐标运算,直线与抛物线的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
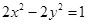 有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .
有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .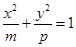 与双曲线
与双曲线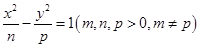 有公共的焦点
有公共的焦点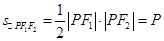
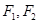 ,其交点为
,其交点为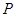 且∠
且∠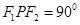 ,则△
,则△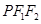 的面积是( )
的面积是( )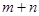 B.
B. 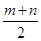 C.
C. 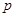 D.
D. 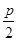
 与双曲线
与双曲线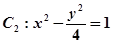 有公共的焦点,
有公共的焦点, 的一条渐近线与以
的一条渐近线与以 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若 =
=