题目内容
已知两点A(-2,0),B(0,2)，点C是圆x2+y2-2x=0上的任意一点，则△ABC的面积最小值是（ ）
A．3- | B．3+ | C． | D． |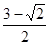
A
试题分析：A(-2,0),B(0,2)，
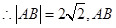直线方程为
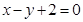，圆x2+y2-2x=0的圆心为
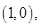半径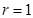
，圆心到直线的距离为
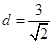，所以圆上的点C到直线的最小距离为
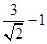，三角形面积最小值为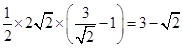
点评：要使三角形面积最小需满足动点C到直线AB的距离最小，借助于圆的中心对称性可求得最小距离
练习册系列答案
阅读快车系列答案
相关题目
函数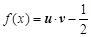
的最小正周期为
.
的值；
在区间
上的值域.
.
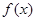的最小值，并求使
的集合；
的图像可由
的图象经过怎样的变化得到.
），其中ω＞0，｜
，若cos
cos
sin
．
．
的最小正周期及其单调增区间：
时，求
的结果是（ ）
的最大值为 ；