题目内容
12. 如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )| A. | y2=$\frac{5}{4}$x | B. | y2=$\frac{5}{2}$x | C. | y2=5x | D. | y2=10x |
分析 利用OD⊥AB,可求直线AB的方程,与抛物线方程联立,利用韦达定理,结合OA⊥OB,利用向量的数量积公式,即可求出p的值.
解答 解:∵OD⊥AB,∴kOD•kAB=-1.
又kOD=$\frac{1}{2}$,∴kAB=-2,
∴直线AB的方程为y=-2x+5,
设A(x1,x2),B(x2,y2),则
由OA⊥OB,即$\overrightarrow{OA}$⊥$\overrightarrow{OB}$.
则x1x2+y1y2=0,
又x1x2+y1y2=x1x2+(-2x1+5)(-2x2+5)=5x1x2-10(x1+x2)+25=0,
联立方程$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=-2x+5}\end{array}\right.$,
消y可得4x2-(20+2p)x+25=0①
∴x1+x2=$\frac{10+p}{2}$,x1x2=$\frac{25}{4}$.
∴x1x2+y1y2=5×$\frac{25}{4}$-10×$\frac{10+p}{2}$+25=0,
∴p=$\frac{5}{4}$,
当p=$\frac{5}{4}$时,方程①成为8x2-45x+50=0显然此方程有解.
∴p=$\frac{5}{4}$成立,
即有抛物线的方程为y2=$\frac{5}{2}$x.
故选B.
点评 本题主要考查抛物线方程,同时考查直线与抛物线的位置关系,正确运用韦达定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.过抛物线y2=2px(p>0)的焦点F的直线l,依次分别交抛物线的准线、y轴、抛物线于A、B、C三点.若$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,则直线l的斜率是( )
| A. | $-\sqrt{2}$或$\sqrt{2}$ | B. | -2或2 | C. | $-2\sqrt{2}$或$2\sqrt{2}$ | D. | -4或4 |
17.某种图书每册的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
检测每册书的成本费y与印刷册数的倒数$\frac{1}{x}$之间是否具有线性相关关系,如有,求出y与x的回归方程.
| x | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | 100 | 200 |
| y | 10.15 | 5.52 | 4.08 | 2.85 | 2.11 | 1.62 | 1.41 | 1.30 | 1.21 | 1.15 |
 .
. 中,已知
中,已知 ,点
,点 和点
和点 分别在线段
分别在线段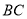 和
和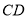 上,且
上,且 ,则
,则 的值为_____________.
的值为_____________.
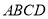 中对角线
中对角线 为
为 的中点,则
的中点,则 ( )
( )