题目内容
如图,在 中,
中, ,
, 是
是 上的一点,若
上的一点,若 ,则实数
,则实数 的值为( )
的值为( )








C
解析考点:平面向量的基本定理及其意义.
分析:由已知中△ABC中, ,P是BN上的一点,设
,P是BN上的一点,设  =λ
=λ 后,我们易将
后,我们易将 表示为(1-λ)
表示为(1-λ)  +
+ 
 的形式,根据平面向量的基本定理我们易构造关于λ,m的方程组,解方程组后即可得到m的值
的形式,根据平面向量的基本定理我们易构造关于λ,m的方程组,解方程组后即可得到m的值
解:∵P是BN上的一点,
设 =λ
=λ ,由
,由 ,
,
则 =
= +
+
= +λ
+λ
= +λ(
+λ( -
- )
)
="(1-λ)"  +λ
+λ
="(1-λ)"  +
+ 

=m +
+

∴m=1-λ, =
=
解得λ= ,m=
,m=
故选C

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
在平行四边形 中,点
中,点 为
为 中点,
中点, ,则
,则 等于
等于
A. | B. | C. | D. |
 是
是 的
的 边上的中线,若
边上的中线,若 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D.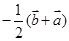 |
已知 ,
,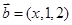 ,且
,且 ,则
,则
A. | B. | C. | D. |
设向量 的( )
的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若A(-2,3),B(3,-2),C( ,m)三点共线,则m的值为 ( )
,m)三点共线,则m的值为 ( )
A. | B.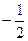 | C.-2 | D.2 |
已知 ,
, ,且
,且 ,则点
,则点 的坐标为 ( )
的坐标为 ( )
A. | B. | C. | D. |
 为等腰三角形,
为等腰三角形, ,
,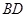 为
为 边上的高,若
边上的高,若
 ,
,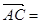
 ,则
,则





 ︱=1,︱
︱=1,︱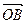 ︱=
︱= ,
, =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设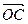 =m
=m 等于
等于