题目内容
球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2
的正三角形,平面SAB⊥平面ABC,则棱锥S-ABC的体积的最大值为( )
| 3 |
分析:由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,当S在“最高点”,也就是说H为AB中点时,SH最大,棱锥S-ABC的体积最大.
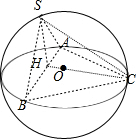
解答:解:由题意画出几何体的图形如图
由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,
当S在“最高点”,也就是说H为AB中点时,SH最大,棱锥S-ABC的体积最大.
∵△ABC是边长为2
的正三角形,
∴球的半径r=OC=
CH=
×
×2
=2,
在RT△SHO中,OH=
OC=
OS=1,
∴∠HSO=30°,求得SH=OScos30°=
,
∴体积V=
Sh=
×
×2
×2
×
×
=3.
故选A.
由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,
当S在“最高点”,也就是说H为AB中点时,SH最大,棱锥S-ABC的体积最大.
∵△ABC是边长为2
| 3 |
∴球的半径r=OC=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
在RT△SHO中,OH=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠HSO=30°,求得SH=OScos30°=
| 3 |
∴体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
故选A.

点评:本题考查锥体体积计算,根据几何体的结构特征确定出S位置是关键.考查空间想象能力、计算能力.

练习册系列答案
相关题目







