题目内容
设
的内角
所对边的长分别为
若
，则角
（ ）
A． | B． | C． | D． |
B
解析试题分析：由于的内角所对边的长分别为若.所以有正弦定理可得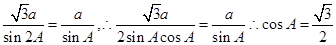
.又因为
.所以
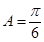.故选B.
考点：1.正弦定理.2.三角函数的二倍角公式.3.解三角方程
练习册系列答案
相关题目
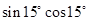值为（ ）
A． | B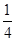． | C． | D． |
在△ABC中，
，
，
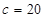，则边
的长为（ ）
A． | B． | C． | D． |
在
中，
，则
等于
| A．30° | B．60° |
| C．60°或120° | D．30°或150 |
后，就可以计算出A、B两点的距离为（ ）
B．
D．
设
的内角
所对的边分别为
，已知
，
，则角
的大小为
A． | B． | C． | D．或 |
在△ABC中，内角A，B，C所对的边分别是a，b，c.已知8b＝5c，C＝2B，则cos C＝( )．
A． | B．－ | C．± | D． |
在△ABC中，a，b，c分别为角A，B，C所对的边，若ccos A＝b，则△ABC( )．
| A．一定是锐角三角形 | B．一定是钝角三角形 |
| C．一定是直角三角形 | D．一定是斜三角形 |
sin Asin C，则角B为 ( )．
