题目内容
已知双曲线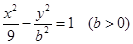 的一个焦点坐标是
的一个焦点坐标是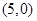 ,则
,则 等于( ).
等于( ).
A. | B.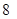 | C.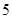 | D.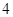 |
D
解析考点:双曲线的简单性质.
分析:由双曲线的标准方程可求得a,b,由a、b、c 的关系表示出 c,由已知焦点坐标可求得c.
解:由双曲线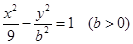 的一个焦点坐标为 (5,0),
的一个焦点坐标为 (5,0),
得a=3,c=5,
∴b=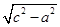 =
=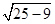 =4,
=4,
故选D

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
抛物线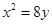 的准线方程为( )
的准线方程为( )
A.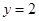 | B.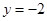 | C.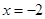 | D.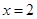 |
若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )
A.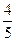 | B.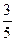 | C.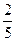 | D.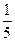 |
双曲线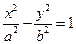 的渐近线与圆
的渐近线与圆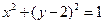 相切,则双曲线离心率为
相切,则双曲线离心率为
A.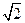 | B.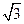 | C.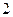 | D.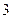 |
抛物线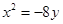 的准线方程为
的准线方程为
| A.x=2 | B.x= 2 2 | C.y=2 | D.y= 2 2 |
.设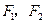 分别是椭圆
分别是椭圆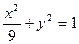
 的左、右焦点.若点
的左、右焦点.若点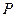 在椭圆上,且
在椭圆上,且 ,则
,则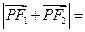
A.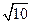 | B.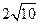 | C.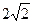 | D.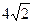 |
下列曲线中离心率为 的是 ( )
的是 ( )
A.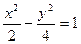 | B.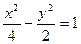 |
C.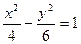 | D.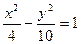 |
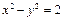 绕原点逆时针旋转
绕原点逆时针旋转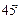 后可得到双曲线
后可得到双曲线 .据此类推可求得双曲线
.据此类推可求得双曲线 的焦距为
的焦距为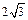



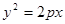 的焦点与椭圆
的焦点与椭圆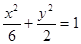 的右焦点重合,则
的右焦点重合,则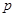 的值为 ( )
的值为 ( )