题目内容
一个圆环直径为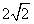 m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
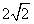 m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。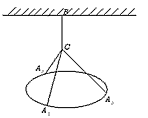
(Ⅰ)设BC长为x(m),铁丝总长为y(m),试写出y关于x的函数解析式,并写出函数的定义域;
(Ⅱ)当x取多长时,铁丝总长y有最小值,并求此最小值。
(Ⅱ)当x取多长时,铁丝总长y有最小值,并求此最小值。
解:(Ⅰ)由题意C, 四点构成一个正三棱锥,
四点构成一个正三棱锥, 为该三棱锥的三条侧棱,
为该三棱锥的三条侧棱,
三棱锥的侧棱 ,
,
于是 (0<x<2)。
(0<x<2)。
(Ⅱ)对y求导,得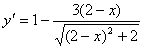 ,
,
令 ,得
,得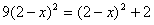 ,解得:
,解得: 或
或 (舍),
(舍),
当 时,
时, ;
;
当 时,
时, ,
,
故当 时,即BC=1.5m时,y取得最小值为6m。
时,即BC=1.5m时,y取得最小值为6m。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
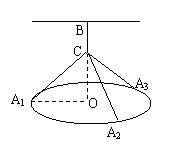 (2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
(2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.