题目内容
已知椭圆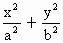 =1(a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+
=1(a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+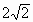 =0的距离为3.
=0的距离为3.
(Ⅰ)求该椭圆的方程;
(Ⅱ)是否存在斜率不为0的直线l,使其与已知椭圆交于M、N两点,满足AM⊥AN,且|AM|=|AN|.
(Ⅲ)若斜率为k的直线l与椭圆交于M,N两点,使得|AM|=|AN|,求k的取值范围.
答案:
解析:
解析:
|
(Ⅰ)由已知b=1. 又椭圆右焦点F(c,0)到直线x-y+
∴c= 可得 故椭圆的方程为 (Ⅱ)不存在. 若存在直线l∶y=kx+m(k≠0)满足条件,则建立方程组
消去y,得( 判别式 △= 即 设 M( 由方程①及韦达定理,有
由直线l的方程,得 ∴MN中点B的坐标为( 又由|AM|=|AN|,有AB⊥MN, ∴ 化简后得 m= 于是中点B的坐标为( 不等式②可化为 (-12)× 即 9( 解得 -1<k<1.(k≠0) 若AM⊥AN,则|AB|=
又 ∴
由
即
故 满足条件的直线l不存在. (Ⅲ)设直线l的方程为y=kx+m, 建立方程组 消去y,得 判别式 △= 即 设 由方程①及韦达定理,有
代入直线l的方程,得 ∴MN中点B的坐标为( 又由|AM|=|AN|,有 AB⊥MN, ∴ 化简后得 m= 不等式②可化为 (-12)× 即 解得 -1<k<1. 故 直线l的斜率k的取值范围为(-1,1). |

练习册系列答案
相关题目
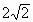 =0的距离为
=0的距离为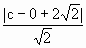 =3.
=3.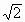 .
.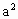 =3.
=3.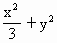 =1.
=1.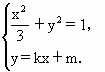
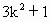 )
)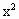 +6kmx+3(
+6kmx+3(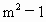 )=0.…………①
)=0.…………①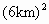 -4(
-4(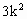 +1)×3(
+1)×3(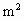 -1)>0.
-1)>0.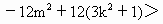 0.……………②
0.……………②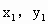 )、N(
)、N(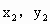 ),MN的中点为B,
),MN的中点为B,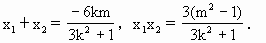
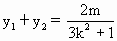
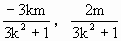 ).
).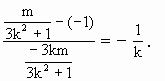
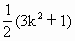 .
.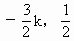 ).
).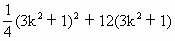 >0,
>0,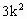 +1)(1-
+1)(1-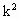 )>0.
)>0.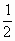 |MN|.
|MN|. ,
,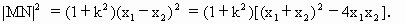
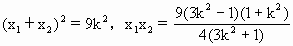
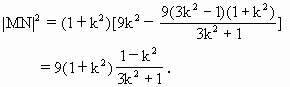
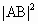 =
=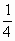 =
=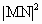 ,
,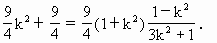
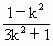 =1.
=1.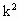 =0,与题设k≠0矛盾.
=0,与题设k≠0矛盾.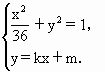
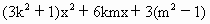 =0,①
=0,①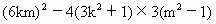 >0,
>0,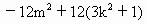 >0,②
>0,②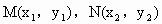 ,MN的中点为B,
,MN的中点为B,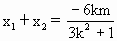
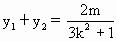 ,
,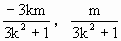 ).
).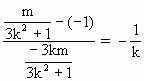 .
.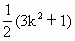 ,
,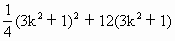 >0,
>0,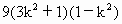 >0,
>0, =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,则双曲线
,则双曲线 =1的离心率为
=1的离心率为

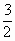

 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4( +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 

