题目内容
ABCD与CDEF是两个全等的正方形，且两个正方形所在平面互相垂直，M是BC的中点，则异面直线AM与DF所成角的正切值为分析：画出图形，作出异面直线所成的角，利用三面角公式求出所求角的余弦值，然后求出所求结果．
解答：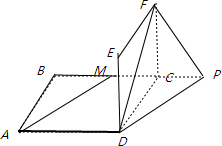
解：如图所示，延长MC至P，使得PC=MC，连接DP，
则异面直线AM与DF所成角就是∠PDF，由三面角公式可得：
cos∠PDF=cos45°•cos∠CDP=
×
=
所以tan∠PDF=
=
=
故答案为：
．
解：如图所示，延长MC至P，使得PC=MC，连接DP，则异面直线AM与DF所成角就是∠PDF，由三面角公式可得：
cos∠PDF=cos45°•cos∠CDP=
| ||
| 2 |
2
| ||
| 5 |
| ||
| 5 |
所以tan∠PDF=
| sin∠PDF |
| cos∠PDF |
| ||||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题是中档题，考查异面直线所成角的大小的求法，注意异面直线的定义，是求解这类题型的主要方法，注意三面角公式的应用，简化解题过程．
练习册系列答案
相关题目