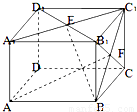
题目内容
在长方体AC1中,AA1=AD=2,AB=4,M、N分别是AB与BC的中点,则直线A1M与C1N的位置关系是
.
相交
相交
; 它们所成角的大小是arccos
| ||
| 5 |
arccos
;点A到对角线B1D的距离是
| ||
| 5 |
| ||
| 3 |
| ||
| 3 |
分析:①连接A1C1,MN,由题意可得:MN∥A1C1,并且MN=
A1C1,进而得到直线A1M与C1N相交.
②取A1B1,B1C1的中点分别为E,F,连接BE,NF,可得BE∥A1M,BF∥C1N,所以∠EBF与所求角相等或者互补,再利用解三角形的有关知识求出答案.
③设点A到对角线B1D的距离是 h,根据长方体的结构特征可得:AB1⊥AD,可得△AB1D为直角三角形,进而根据等面积法可得答案.
| 1 |
| 2 |
②取A1B1,B1C1的中点分别为E,F,连接BE,NF,可得BE∥A1M,BF∥C1N,所以∠EBF与所求角相等或者互补,再利用解三角形的有关知识求出答案.
③设点A到对角线B1D的距离是 h,根据长方体的结构特征可得:AB1⊥AD,可得△AB1D为直角三角形,进而根据等面积法可得答案.
解答:解:长方体如图所示:
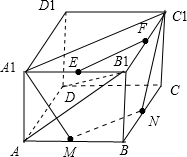
①连接A1C1,MN,
因为在长方体AC1中,M、N分别是AB与BC的中点,
所以MN∥A1C1,并且MN=
A1C1,
所以直线A1M与C1N相交,
所以直线A1M与C1N的位置关系是:相交.
②取A1B1,B1C1的中点分别为E,F,连接BE,NF,
因为M,E分别为AB,A1B1的中点,
所以BE∥A1M,同理BF∥C1N,
所以∠EBF与所求角相等或者互补.
因为在长方体AC1中,AA1=AD=2,AB=4,
所以在△BEF中有:BE=2
,BF=
,EF=
,
所以cos∠EBF=
,
所以直线A1M与C1N所成角的大小是arccos
.
③设点A到对角线B1D的距离是 h,
根据长方体的结构特征可得:AB1⊥AD,
所以△AB1D为直角三角形,并且AD=2,AB1=2
,B1D=2
,
所以根据等面积法可得:h=
=
.
故答案为:相交;arccos
;
.

①连接A1C1,MN,
因为在长方体AC1中,M、N分别是AB与BC的中点,
所以MN∥A1C1,并且MN=
| 1 |
| 2 |
所以直线A1M与C1N相交,
所以直线A1M与C1N的位置关系是:相交.
②取A1B1,B1C1的中点分别为E,F,连接BE,NF,
因为M,E分别为AB,A1B1的中点,
所以BE∥A1M,同理BF∥C1N,
所以∠EBF与所求角相等或者互补.
因为在长方体AC1中,AA1=AD=2,AB=4,
所以在△BEF中有:BE=2
| 2 |
| 5 |
| 5 |
所以cos∠EBF=
| ||
| 5 |
所以直线A1M与C1N所成角的大小是arccos
| ||
| 5 |
③设点A到对角线B1D的距离是 h,
根据长方体的结构特征可得:AB1⊥AD,
所以△AB1D为直角三角形,并且AD=2,AB1=2
| 5 |
| 6 |
所以根据等面积法可得:h=
| AD•AB1 |
| B1D |
| ||
| 3 |
故答案为:相交;arccos
| ||
| 5 |
| ||
| 3 |
点评:解决此类问题的关键是熟练掌握长方体的结构特征与空间中点、线、面得位置关系的判定,以及求空间角(平移法)与空间距离(等积法)的方法,也可以距离空间直角坐标系,利用空间向量的有关运算求空间角与空间距离,以及判断线面的位置关系.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,在长方体AC1中,AB=BC=2,
如图,在长方体AC1中,AB=BC=2, 长方体AC1中,AB=BC=1,AA1=2,过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于
长方体AC1中,AB=BC=1,AA1=2,过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于 ,这样的直线最多可作 ______条.
,这样的直线最多可作 ______条. ,E,F分别是面A1C1.面BC1的中心,则AF和BE所成的角为( )
,E,F分别是面A1C1.面BC1的中心,则AF和BE所成的角为( )