Question

9．给出下列关于椭圆的真命题，试类比推理给出双曲线中类似的命题，并画出命题中的图．
（1）椭圆中以焦半径为直径的圆与长轴为直径的圆相切（此圆与椭圆内切）；
（2）椭圆互相垂直的焦点弦倒数之和为常数$\frac{1}{|AB|}$+$\frac{1}{|CD|}$=$\frac{2-{e}^{2}}{2ep}$；
（3）设椭圆焦点弦AB的中垂线交长轴于点D，则|DF|与|AB|之比为离心率的一半（F为焦点）．

Answer 1

分析 由题目给出的椭圆的几何性质，类比得到双曲线的几何性质，并作出图形得答案．

解答 解：（1）类比推理为：以双曲线的一条焦半径为直径的圆与以实轴为直径的圆内切或外切．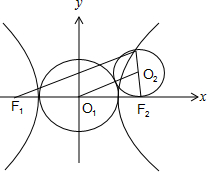

（2）类比推理为：双曲线互相垂直的焦点弦倒数之和为常数$\frac{1}{|AB|}$+$\frac{1}{|CD|}$=$\frac{|2-{e}^{2}|}{2ep}$．

（3）设双曲线焦点弦AB的中垂线交实轴于点D，则|DF|与|AB|之比为离心率的一半（F为焦点）．

点评 本题考查椭圆和双曲线的简单性质，考查了类比推理，训练了作图能力，是中档题．