题目内容
从集合U={a,b,c,d}的子集中选出4个不同的子集,需同时满足以下两个条件:
(1)∅,U都要选出;
(2)对选出的任意两个子集A和B,必有A⊆B或B⊆A,
则不同的选法种数是( )
(1)∅,U都要选出;
(2)对选出的任意两个子集A和B,必有A⊆B或B⊆A,
则不同的选法种数是( )
分析:由题意知,子集A和B可以互换,即视为一种选法,从而对子集A分类讨论,确定B相应的结果,根据计数原理得到结论.
解答:解:因为∅,U都要选出而所有任意两个子集的组合必须有包含关系,故各个子集所包含的元素个数必须依次递增,
因为必须包含空集和全集,所以需要选择的子集有两个
设第二个子集的元素个数为1,有(a)(b)(c)(d)四种选法
(1)第三个子集元素个数为2,当第二个子集为(a)时,第三个子集的2个元素中必须包含a,剩下的一个从bcd中选取
有三种选法,所以这种子集的选取方法共有4×3=12种
(2)第三个子集中包含3个元素,同理三个元素必须有一个与第二个子集中的元素相同,共有4×3=12种
(3)第二个子集有两个元素,有6种取法,第三个子集必须有3个元素且必须包含前面一个子集的两个元素,有两种取法
所以这种方法有6×2=12种
综上一共有12+12+12=36种
故选B.
因为必须包含空集和全集,所以需要选择的子集有两个
设第二个子集的元素个数为1,有(a)(b)(c)(d)四种选法
(1)第三个子集元素个数为2,当第二个子集为(a)时,第三个子集的2个元素中必须包含a,剩下的一个从bcd中选取
有三种选法,所以这种子集的选取方法共有4×3=12种
(2)第三个子集中包含3个元素,同理三个元素必须有一个与第二个子集中的元素相同,共有4×3=12种
(3)第二个子集有两个元素,有6种取法,第三个子集必须有3个元素且必须包含前面一个子集的两个元素,有两种取法
所以这种方法有6×2=12种
综上一共有12+12+12=36种
故选B.
点评:本题考查集合的子集及利用排列组合知识解决实际问题,考查分析问题与解决问题的能力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
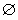 ,U都要选出;
,U都要选出;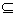 B或A
B或A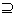 B;
B;