题目内容
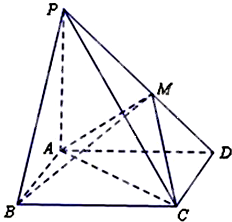 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD,垂足为M.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD,垂足为M.(Ⅰ)求证:AM⊥PD;
(Ⅱ)求三棱锥B-AMC的体积;
(III)已知点N在AC上,当N 点在什么位置时,使得MN∥平面PBC.
分析:(Ⅰ)要证AM⊥PD,只要证明PD⊥平面AMB 即可,因为已知BM⊥PD,所以只要证明PD⊥AB即可,为此需要证明AB⊥平面PAD,由已知条件可以得出;
(Ⅱ)要计算三棱锥B-AMC的体积,只要求出把△BAC作为底面时的高即可,只要作MH⊥AD,则可以证明MH⊥底面ABCD;
(Ⅲ)点N在AC上,使得MN∥平面PBC,只要理解对角线BD与AC相较于一点N,利用三角形的中位线可以证出.
(Ⅱ)要计算三棱锥B-AMC的体积,只要求出把△BAC作为底面时的高即可,只要作MH⊥AD,则可以证明MH⊥底面ABCD;
(Ⅲ)点N在AC上,使得MN∥平面PBC,只要理解对角线BD与AC相较于一点N,利用三角形的中位线可以证出.
解答:解:(Ⅰ)证明:∵PA⊥平面ABCD,∴PA⊥AB.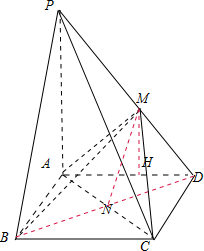
又∵BA⊥AD,AD∩PA=A,
∴AB⊥平面PAD,∴AB⊥PD.
∵BM⊥PD,AB∩BM=B,
∴PD⊥平面ABM.
∴PD⊥AM.
(Ⅱ)由(Ⅰ)可知:AM⊥PD.
∵在△PAD中,AP=AD=2,∴M是PD的中点.
过点M作MH⊥AD,则MH⊥底面ABCD,且MH=
AP=1.
∴V三棱锥B-AMC=
×S△ABC×MH=
×
×2×1×1=
.
(Ⅲ)连接BD,交AC于点N,当点N为对角线AC与BD的交点时,满足MN∥平面PBC.
证明:∵PM=MD,BN=ND,∴MN∥PB.
又MN?平面PBC,PB?平面PBC,
∴MN∥平面PBC.

又∵BA⊥AD,AD∩PA=A,
∴AB⊥平面PAD,∴AB⊥PD.
∵BM⊥PD,AB∩BM=B,
∴PD⊥平面ABM.
∴PD⊥AM.
(Ⅱ)由(Ⅰ)可知:AM⊥PD.
∵在△PAD中,AP=AD=2,∴M是PD的中点.
过点M作MH⊥AD,则MH⊥底面ABCD,且MH=
| 1 |
| 2 |
∴V三棱锥B-AMC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(Ⅲ)连接BD,交AC于点N,当点N为对角线AC与BD的交点时,满足MN∥平面PBC.
证明:∵PM=MD,BN=ND,∴MN∥PB.
又MN?平面PBC,PB?平面PBC,
∴MN∥平面PBC.
点评:熟练掌握线面平行与垂直的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
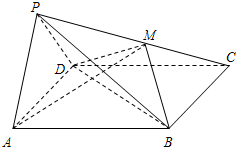 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.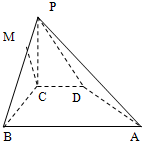 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB