题目内容
设 的三个内角
的三个内角 所对的边分别为
所对的边分别为 .已知
.已知 .
.
(1)求角A的大小;(2)若 ,求
,求 的最大值.
的最大值.
【答案】
(1) ;(2)
;(2)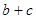 取得最大值4.
取得最大值4.
【解析】本试题主要考查运用两角和差的正弦公式来求解得到角A的值,并结合正弦定理和三角函数性质得到最值
(1)利用两角差的正弦公式可知得到A的正切值,从而得到角A
(2)既可以运用余弦定理结合不等式求解最值,也可以利用三角函数,将边化为角,利用函数的值域得到最值。
解:(Ⅰ)由已知有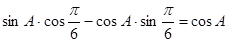 ,
,
故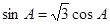 ,
,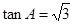 .
.
又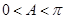 ,所以
,所以 .
.
(Ⅱ)由正弦定理得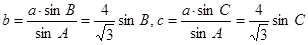 ,
,
故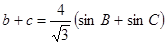 .………………………………8分
.………………………………8分

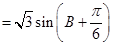 .………………………………10分
.………………………………10分
所以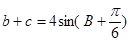 .
.
因为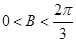 ,所以
,所以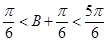 .
.
∴当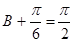 即
即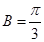 时,
时,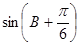 取得最大值
取得最大值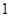 ,
,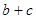 取得最大值4. …………12分
取得最大值4. …………12分
解法二:(Ⅰ)同解法一.
(Ⅱ)由余弦定理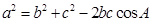 得,
得, ,………………………………8分
,………………………………8分
所以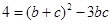 ,即
,即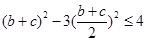 ,………………………………10分
,………………………………10分
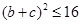 ,故
,故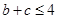 .
.
所以,当且仅当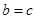 ,即
,即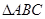 为正三角形时,
为正三角形时,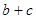 取得最大值4. …………12
取得最大值4. …………12

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
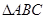 的三个内角
的三个内角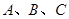 所对的边分别为
所对的边分别为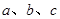 ,且满足
,且满足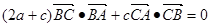 .
.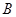 的大小;
的大小;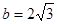 ,试求
,试求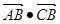 的最小值.
的最小值.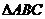 的三个内角
的三个内角 所对的边分别为
所对的边分别为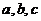 .已知
.已知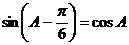 .
. ,求
,求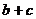 的最大值.
的最大值.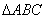 的三个内角
的三个内角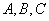 所对的边分别为
所对的边分别为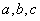 ,且满足
,且满足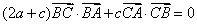 .
.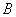 的大小;
的大小;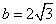 ,试求
,试求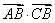 的最小值.
的最小值.