题目内容
若函数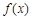 为定义域
为定义域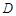 上单调函数,且存在区间
上单调函数,且存在区间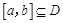 (其中
(其中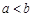 ),使得当
),使得当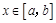 时,
时,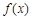 的取值范围恰为
的取值范围恰为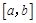 ,则称函数
,则称函数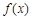 是
是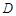 上的正函数,区间
上的正函数,区间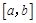 叫做等域区间.
叫做等域区间.
(1)已知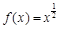 是
是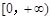 上的正函数,求
上的正函数,求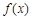 的等域区间;
的等域区间;
(2)试探究是否存在实数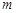 ,使得函数
,使得函数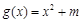 是
是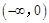 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数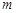 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由
【答案】
(1)因为 是
是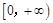 上的正函数,且
上的正函数,且 在
在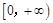 上单调递增,
上单调递增,
所以当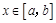 时,
时,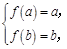 即
即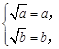
解得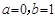 ,
,
故函数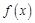 的“等域区间”为
的“等域区间”为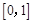 ;
;
(2)因为函数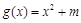 是
是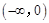 上的减函数,
上的减函数,
所以当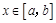 时,
时,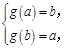 即
即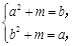
两式相减得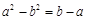 ,即
,即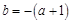 ,
,
代入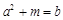 得
得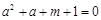 ,
,
由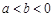 ,且
,且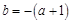 得
得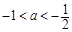 ,
,
故关于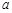 的方程
的方程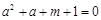 在区间
在区间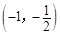 内有实数解,
内有实数解,
记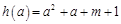 ,
,
则 解得
解得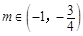 .
.
【解析】略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 为定义域
为定义域 上单调函数,且存在区间
上单调函数,且存在区间 (其中
(其中 ),使得当
),使得当 时,
时, ,则称函数
,则称函数 是
是 上的正函数,则实数
上的正函数,则实数 的取值范围 ▲
.
的取值范围 ▲
.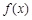 为定义域
为定义域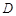 上单调函数,且存在区间
上单调函数,且存在区间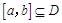 (其中
(其中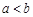 ),使得当
),使得当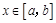 时,
时,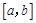 ,则称函数
,则称函数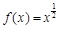 是
是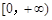 上的正函数,求
上的正函数,求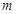 ,使得函数
,使得函数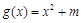 是
是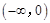 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数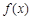 为定义域
为定义域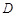 上单调函数,且存在区间
上单调函数,且存在区间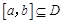 (其中
(其中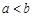 ),使得当
),使得当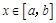 时,
时,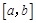 ,则称函数
,则称函数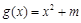 是
是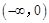 上的正函数,则实数
上的正函数,则实数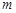 的取值范围为 ▲ .
的取值范围为 ▲ .