题目内容
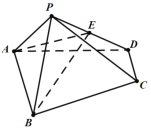
【题目】如图，在四棱锥
中，
∥AB，
，
，
，
，
，
，E是
的中点.
（1）求证：
；
（2）求二面角
的余弦值.
【答案】（1）见解析（2）
【解析】
（1）通过证明
和
，得
平面
，从而即可得到本题答案；
（2）以M点为原点，
为x轴，
为y轴，以过点M且垂直平面ABCD的方向为z轴，建立空间直角坐标系，分别求出平面ABE和平面PBE的法向量，然后套用公式即可得到本题答案.
（1）证明：如图，设M是
的中点，连接
，
在梯形
中，由已知易得，
在
中，
，则，
与
是平面内的两条相交直线，
所以平面，而
在平面内，
所以
；
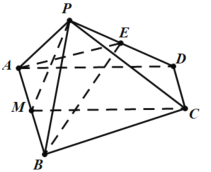
（2）解：作PH垂直于MC，垂足为H，以M点为原点，为x轴，为y轴，以过点M且垂直平面ABCD的方向为z轴，建立空间直角坐标系.
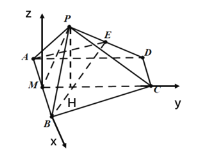
在
中，因为
,
,所以
，则
，
易知
，又
，所以
，即
为直角三角形，
易得
，
所以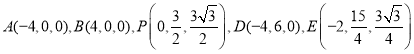
因为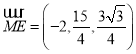
，
所以平面
的一个法向量是
，
又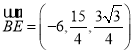
，
，
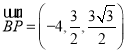所以平面
的一个法向量是
，
，
由图可知，二面角
为锐角，所以二面角的余弦值是.
【题目】2020年3月，国内新冠肺炎疫情得到有效控制，人们开始走出家门享受春光.某旅游景点为吸引游客，推出团体购票优惠方案如下表：
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票，则共需支付门票费1290元；若合并成个团队购票，则需支付门票费990元，那么这两个旅游团队的人数之差为（ ）
A.20B.25C.30D.40
【题目】为了解高中学生对数学课是否喜爱是否和性别有关，随机调查220名高中学生，将他们的意见进行了统计，得到如下的
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
（1）根据上面的列联表判断，能否有
的把握认为“喜爱数学课与性别”有关；
（2）为培养学习兴趣，从不喜爱数学课的学生中进行进一步了解，从上述调查的不喜爱数学课的人员中按分层抽样抽取6人，再从这6人中随机抽出2名进行电话回访，求抽到的2人中至少有1名“男生”的概率.
参考公式：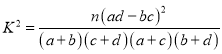
.
P（ | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】假如你的公司计划购买台机器，该种机器使用三年后即被淘汰，在购进机器时，可以一次性额外购买几次维修服务，每次维修服务费用200元，另外实际维修一次还需向维修人员支付小费，小费每次50元，在机器使用期间，如果维修次数超过购机时购买的维修服务次数，则每维修一次需支付维修服务费用500元，无需支付小费，现需决策在购买机器时应同时一次性购买几次维修服务，为此搜集并整理了100台这种机器在三年使用期内的维修次数，得下面统计表：
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记
表示1台机器在三年使用期内的维修次数，
表示1台机器在维修上所需的费用（单位：元），
表示购机的同时购买的维修服务次数.
（1）若
，求与的函数解析式.
（2）若要求“维修次数不大于”的频率不小于0.8，求的值.
（3）假设这100台机器在购机的同时每台都购买10次维修服务，或每台都购买11次维修服务，分别计算这100台机器在维修上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买10次还是11次维修服务？
