题目内容
张家界某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值y万元与投入x(x≥10)万元之间满足:y=f(x)=ax2+| 101 |
| 50 |
| x |
| 10 |
(1)求f(x)的解析式;
(2)求该景点改造升级后旅游利润T(x)的最大值.(利润=旅游增加值-投入)
分析:(1)由条件:“当x=10万元时,y=19.2万元;当x=20万元时,y=35.7万元”列出关于a,b的方程,解得a,b的值即得则求f(x)的解析式;
(2)先写出函数T(x)的解析式,再利用导数研究其单调性,进而得出其最大值,从而解决问题.
(2)先写出函数T(x)的解析式,再利用导数研究其单调性,进而得出其最大值,从而解决问题.
解答:解:(1)由条件
(2分)
解得a=-
,b=1(4分)
则f(x)=-
+
x-ln
(x≥10).(6分)
(2)由T(x)=f(x)-x=-
+
x-ln
(x≥10)
则T′(x)=
+
-
=-
(10分)
令T'(x)=0,则x=1(舍)或x=50
当x∈(10,50)时,T'(x)>0,
因此T(x)在(10,50)上是增函数;
当
•
=x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2时,T'(x)<0,
因此T(x)在(50,+∞)上是减函数,∴x=50为T(x)的极大值点(12分)
即该景点改造升级后旅游利润T(x))的最大值为T(50)=24.4万元.(13分)
|
解得a=-
| 1 |
| 100 |
则f(x)=-
| x2 |
| 100 |
| 101 |
| 50 |
| x |
| 10 |
(2)由T(x)=f(x)-x=-
| x2 |
| 100 |
| 51 |
| 50 |
| x |
| 10 |
则T′(x)=
| -x |
| 50 |
| 51 |
| 50 |
| 1 |
| x |
| (x-1)(x-50) |
| 50x |
令T'(x)=0,则x=1(舍)或x=50
当x∈(10,50)时,T'(x)>0,
因此T(x)在(10,50)上是增函数;
当
| MA |
| MB |
因此T(x)在(50,+∞)上是减函数,∴x=50为T(x)的极大值点(12分)
即该景点改造升级后旅游利润T(x))的最大值为T(50)=24.4万元.(13分)
点评:本小题主要考查函数模型的选择与应用、应用所学导数的知识、思想和方法解决实际问题的能力,建立函数式、解方程、不等式、最大值等基础知识.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
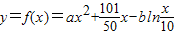 ,a,b为常数.当x=10万元时,y=19.2万元;当x=20万元时,y=35.7万元.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)
,a,b为常数.当x=10万元时,y=19.2万元;当x=20万元时,y=35.7万元.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)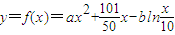 ,a,b为常数.当x=10万元时,y=19.2万元;当x=20万元时,y=35.7万元.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)
,a,b为常数.当x=10万元时,y=19.2万元;当x=20万元时,y=35.7万元.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6) 万元与投入
万元与投入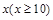 万元之间满足:
万元之间满足: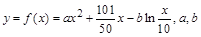 为常数。当
为常数。当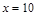 万元时,
万元时, 万元;当
万元;当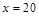 万元时,
万元时,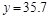 万元。(参考数据:
万元。(参考数据: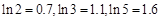 )
)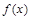 的解析式;
的解析式;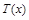 的最大值。(利润=旅游增加值-投入)
的最大值。(利润=旅游增加值-投入) 万元与投入
万元与投入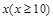 万元之间满足:
万元之间满足: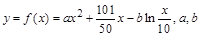 为常数。当
为常数。当 万元时,
万元时,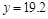 万元;当
万元;当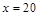 万元时,
万元时, 万元。(参考数据:
万元。(参考数据: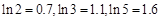 )
)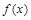 的解析式;
的解析式;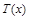 的最大值。(利润=旅游增加值-投入)
的最大值。(利润=旅游增加值-投入)