题目内容
选做题(考生注意:请在(A)(B)两题中,任选做一题作答,若多做,则按(A)题计分)
(A)(参数方程与极坐标选讲)已知在极坐标系下,点A(1,
),B(3,
),O是极点,则△AOB的面积等于
;
(B)关于x的不等式|
|>
的解集是
(A)(参数方程与极坐标选讲)已知在极坐标系下,点A(1,
| π |
| 3 |
| 2π |
| 3 |
3
| ||
| 4 |
3
| ||
| 4 |
(B)关于x的不等式|
| x+1 |
| x-1 |
| x+1 |
| x-1 |
(-1,1)
(-1,1)
.分析:(A)欲求△OAB的面积,根据极角可得三角形的内角∠AOB,由极径得边OA,OB的长,根据三角形的面积公式即可求得.
(B)直接利用绝对值不等式的解法,求出不等式的解即可.
(B)直接利用绝对值不等式的解法,求出不等式的解即可.
解答: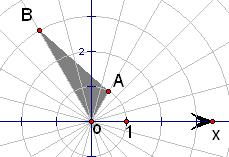 解:(A)由极坐标的意义得:
解:(A)由极坐标的意义得:
△OAB的面积:
OA×OB×sin∠AOB=
×1×3×sin
=
即:△OAB的面积:
.
故答案为:
.
解:(B)因为 |
|>
,所以
<0
解得x∈(-1,1);
故答案为:(-1,1).
 解:(A)由极坐标的意义得:
解:(A)由极坐标的意义得:△OAB的面积:
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
3
| ||
| 4 |
即:△OAB的面积:
3
| ||
| 4 |
故答案为:
3
| ||
| 4 |
解:(B)因为 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
解得x∈(-1,1);
故答案为:(-1,1).
点评:(A)本小题考查点的极坐标的应用,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别.
(B)本小题是基础题,考查绝对值不等式的解法,分式不等式的解法,注意同解变形的应用.
(B)本小题是基础题,考查绝对值不等式的解法,分式不等式的解法,注意同解变形的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则实数
,则实数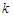 的取值范围是 ;
的取值范围是 ;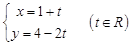 与圆
与圆 相交于AB,则以AB为直径的圆的面积为 .
相交于AB,则以AB为直径的圆的面积为 . ,则实数
,则实数 的取值范围是 ;
的取值范围是 ; 与圆
与圆 相交于AB,则以AB为直径的圆的面积为 .
相交于AB,则以AB为直径的圆的面积为 . ,则实数
,则实数 的取值范围是 ;
的取值范围是 ; 与圆
与圆 相交于AB,则以AB为直径的圆的面积为 .
相交于AB,则以AB为直径的圆的面积为 .