题目内容
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为x,“实用性”得分为y,统计结果如下表:| y 作品数量 x |
实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 |
1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | 1 | b | 6 | 0 | a | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
(2)若“实用性”得分的数学期望为
| 167 |
| 50 |
分析:(1)由题意从表中可以看出,“创新性4分且实用性3分”的作品数量6件,利用古典概型可知创新性4分且实用性3分”的概率值;
(2)由题意及图表可知“实用性”得y1分,2分,3分,4分5分,五个等级,且每个等级分别5件,b+4件,15件,15件,a+8件,利用古典概型求出每一个值对应的事件的概率,利用分布列及期望定义即可求得.
(2)由题意及图表可知“实用性”得y1分,2分,3分,4分5分,五个等级,且每个等级分别5件,b+4件,15件,15件,a+8件,利用古典概型求出每一个值对应的事件的概率,利用分布列及期望定义即可求得.
解答:解:(1)从表中可以看出,“创新性4分且实用性3分”的作品数量6件,
∴“创新性4分且实用性3分”的概率
=0.12.
(2)由表可知“实用性”得y1分,2分,3分,4分5分,五个等级,
且每个等级分别5件,b+4件,15件,15件,a+8件.
∴“实用性”得y的分布列为:
又∵“实用性”得分的数学期望
,
∴1×
+2×
+3×
+4×
+5×
=
.
∵作品数量共50件,a+b=3
解a=1,b=2.
∴“创新性4分且实用性3分”的概率
| 6 |
| 50 |
(2)由表可知“实用性”得y1分,2分,3分,4分5分,五个等级,
且每个等级分别5件,b+4件,15件,15件,a+8件.
∴“实用性”得y的分布列为:
| y | 1 | 2 | 3 | 4 | 5 | ||||||||||
| P |
|
|
|
|
|
| 167 |
| 50 |
∴1×
| 5 |
| 50 |
| b+4 |
| 50 |
| 15 |
| 50 |
| 15 |
| 50 |
| a+8 |
| 50 |
| 167 |
| 50 |
∵作品数量共50件,a+b=3
解a=1,b=2.
点评:此题考查了古典概型随机事件的概率公式,离散型随机变量的定义及其分布列,随机变量的期望,还考查了学生的理解与计算能力.

练习册系列答案
相关题目
(本小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为 ,“实用性”得分为
,“实用性”得分为 ,统计结果如下表:
,统计结果如下表:
|
作品数量
|
实用性 |
|||||
|
1分 |
2分 |
3分 |
4分 |
5分 |
||
|
创 新 性 |
1分 |
1 |
3 |
1 |
0 |
1 |
|
2分 |
1 |
0 |
7 |
5 |
1 |
|
|
3分 |
2 |
1 |
0 |
9 |
3 |
|
|
4分 |
1 |
|
6 |
0 |
|
|
|
5分 |
0 |
0 |
1 |
1 |
3 |
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为 ,求
,求 、
、 的值.
的值.
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为x,“实用性”得分为y,统计结果如下表:
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为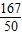 ,求a、b的值.
,求a、b的值.
| y 作品数量 x | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 | 1分 | 1 | 3 | 1 | 1 | |
| 2分 | 1 | 7 | 5 | 1 | ||
| 3分 | 2 | 1 | 9 | 3 | ||
| 4分 | 1 | b | 6 | a | ||
| 5分 | 1 | 1 | 3 | |||
(2)若“实用性”得分的数学期望为
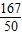 ,求a、b的值.
,求a、b的值.
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为x,“实用性”得分为y,统计结果如下表:
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为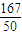 ,求a、b的值.
,求a、b的值.
| y 作品数量 x | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 | 1分 | 1 | 3 | 1 | 1 | |
| 2分 | 1 | 7 | 5 | 1 | ||
| 3分 | 2 | 1 | 9 | 3 | ||
| 4分 | 1 | b | 6 | a | ||
| 5分 | 1 | 1 | 3 | |||
(2)若“实用性”得分的数学期望为
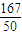 ,求a、b的值.
,求a、b的值. 小题满分12分)
小题满分12分) ,“实用性”得分为
,“实用性”得分为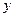 ,统计结果如下表:
,统计结果如下表:

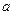
 ,求
,求