题目内容
如图所示,空间四边形ABCD中,E、F、G分别在AB、BC、CD上,且满足AE∶EB=CF∶FB=2∶1,CG∶GD=

3∶1,过E、F、G的平面交AD于H,连接EH.
(1)求AH∶HD;
(2)求证:EH、FG、BD三线共点.
(1)AH∶HD=3∶1(2)证明略
解析:
(1) ∵![]() =
=![]() =2,∴EF∥AC.
=2,∴EF∥AC.
∴EF∥平面ACD.而EF![]() 平面EFGH,
平面EFGH,
且平面EFGH∩平面ACD=GH,
∴EF∥GH.而EF∥AC,
∴AC∥GH.
∴![]()
![]() =
=![]() =3,即AH∶HD=3∶1.
=3,即AH∶HD=3∶1.
(2)证明 ∵EF∥GH,且![]() =
=![]() ,
,![]() =
=![]() ,
,
∴EF≠GH,∴四边形EFGH为梯形.
令EH∩FG=P,则P∈EH,而EH![]() 平面ABD,
平面ABD,
P∈FG,FG![]() 平面BCD,平面ABD∩平面BCD=BD,
平面BCD,平面ABD∩平面BCD=BD,
∴P∈BD.∴EH、FG、BD三线共点.

练习册系列答案
相关题目
 如图所示,空间四边形ABCD中,AB=BD=AD=2,BC=CD=
如图所示,空间四边形ABCD中,AB=BD=AD=2,BC=CD=
| ||
| 2 |
| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
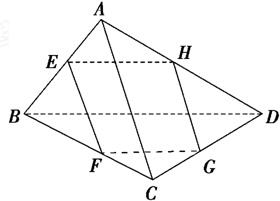 如图所示,空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA上的点,请回答下列问题:
如图所示,空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA上的点,请回答下列问题: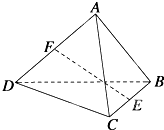 如图所示,空间四边形ABCD中,AB=CD,AB⊥CD,E、F分别为BC、AD的中点,则EF和AB所成的角为
如图所示,空间四边形ABCD中,AB=CD,AB⊥CD,E、F分别为BC、AD的中点,则EF和AB所成的角为