题目内容
将数列{an}的各项排成如图所示的三角形形状.(Ⅰ)若数列{an}是首项为1,公差为2的等差数列,写出图中第5行第5个数;
(Ⅱ)若函数f(x)=a1x+a2x2+a3x3+…+anxn,且f(1)=n2,求数列{an}的通项公式;
(III)设Tm为第m行所有项的和,在(II)的条件下,用含m的代数式表示Tm.

【答案】分析:(Ⅰ)先利用条件求出数列{an}的通项,再判断出第5行第5个数是数列{an}的第15项即可.
(Ⅱ)由f(1)=n2⇒a1+a2+a3++an=n2.就是已知数列{an}的前n项和求其通项公式.代an=Sn-Sn-1 (n≥2)最后检验n=1时通项是否成立即可.
(III)由(Ⅱ)知数列{an}是首项为1,公差为2的等差数列.且第m行所有项构成一个新的首项为m2-m+1,公差为2的等差数列,代入等差数列的求和公式即可.
解答:解:(Ⅰ)由题求得an=1+2(n-1)=2n-1,
又因为第5行第5个数是数列{an}的第15个项,
所以第5行第5个数是29.(2分)
(II)由f(1)=n2,得a1+a2+a3++an=n2.(3分)
设Sn是数列{an}的前n项和,
∴Sn=n2.
当n=1时,a1=S1=1,(5分)
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.(6分)
又当n=1时,2n-1=1=a1,
∴an=2n-1(n=1,2,).(8分)
即数列{an}的通项公式是an=2n-1.
(III)由(II)知数列{an}是首项为1,公差为2的等差数列.(9分)
∵前m-1行共有项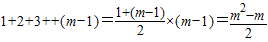 ,
,
∴第m行的第一项为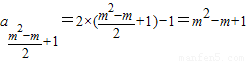 .(11分)
.(11分)
∴第m行构成首项为m2-m+1,公差为2的等差数列,且有m项.
∴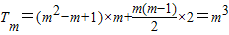 .(13分)
.(13分)
点评:本题是对数列知识的综合考查.且考查了已知前n项和为Sn求数列{an}的通项公式,根据an和Sn的关系:an=Sn-Sn-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:an=Sn-Sn-1 (n≥2);若不成立,则通项公式为分段函数.
(Ⅱ)由f(1)=n2⇒a1+a2+a3++an=n2.就是已知数列{an}的前n项和求其通项公式.代an=Sn-Sn-1 (n≥2)最后检验n=1时通项是否成立即可.
(III)由(Ⅱ)知数列{an}是首项为1,公差为2的等差数列.且第m行所有项构成一个新的首项为m2-m+1,公差为2的等差数列,代入等差数列的求和公式即可.
解答:解:(Ⅰ)由题求得an=1+2(n-1)=2n-1,
又因为第5行第5个数是数列{an}的第15个项,
所以第5行第5个数是29.(2分)
(II)由f(1)=n2,得a1+a2+a3++an=n2.(3分)
设Sn是数列{an}的前n项和,
∴Sn=n2.
当n=1时,a1=S1=1,(5分)
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.(6分)
又当n=1时,2n-1=1=a1,
∴an=2n-1(n=1,2,).(8分)
即数列{an}的通项公式是an=2n-1.
(III)由(II)知数列{an}是首项为1,公差为2的等差数列.(9分)
∵前m-1行共有项
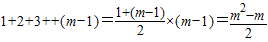 ,
,∴第m行的第一项为
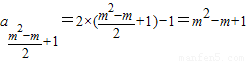 .(11分)
.(11分)∴第m行构成首项为m2-m+1,公差为2的等差数列,且有m项.
∴
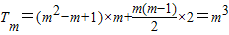 .(13分)
.(13分)点评:本题是对数列知识的综合考查.且考查了已知前n项和为Sn求数列{an}的通项公式,根据an和Sn的关系:an=Sn-Sn-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:an=Sn-Sn-1 (n≥2);若不成立,则通项公式为分段函数.

练习册系列答案
相关题目
 将数列{an}的各项排成如图所示的三角形形状.
将数列{an}的各项排成如图所示的三角形形状.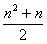 ,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.
,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.
