题目内容
如图,已知面ABC⊥面BCD,AB⊥BC,BC⊥CD,且AB=BC=CD,设AD与面ABC所成角为α,AB与面ACD所成角为β,则α与β的大小关系为( )
分析:由面ABC⊥面BCD,AB⊥BC,BC⊥CD,知DC⊥平面ABC,从而导出α=∠DAC,β=∠BAC,设AB=BC=CD=a,则AC=
a,AD=
a,先求出sinα和sinβ的值,再比较α与β的大小关系.
| 2 |
| 3 |
解答: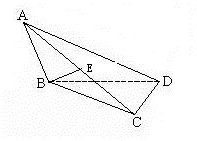 解:∵面ABC⊥面BCD,AB⊥BC,BC⊥CD,
解:∵面ABC⊥面BCD,AB⊥BC,BC⊥CD,
∴DC⊥平面ABC,
∵AD与面ABC所成角为α,∴α=∠DAC,
设AB=BC=CD=a,则AC=
a,AD=
a,
∴sinα=
=
=
.
取AC中点E,∵AB=BC=CD=a,∴BE⊥AC,
∵DC⊥平面ABC,∴BE⊥DC,
∴BE⊥平面ADC,
∵AB与面ACD所成角为β,
∴β=∠BAC,
∴sinβ=
=
=
,
∴α<β,
故选A.
 解:∵面ABC⊥面BCD,AB⊥BC,BC⊥CD,
解:∵面ABC⊥面BCD,AB⊥BC,BC⊥CD,∴DC⊥平面ABC,
∵AD与面ABC所成角为α,∴α=∠DAC,
设AB=BC=CD=a,则AC=
| 2 |
| 3 |
∴sinα=
| CD |
| AD |
| a | ||
|
| ||
| 3 |
取AC中点E,∵AB=BC=CD=a,∴BE⊥AC,
∵DC⊥平面ABC,∴BE⊥DC,
∴BE⊥平面ADC,
∵AB与面ACD所成角为β,
∴β=∠BAC,
∴sinβ=
| BC |
| AC |
| a | ||
|
| ||
| 2 |
∴α<β,
故选A.
点评:本题考查直线与平面所成的角的求法,解题时要认真审题,仔细解答,注意准确找到直线与平面所成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )
(2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )