题目内容
曲线y=Msin(2ωx+φ)+N(M>0,N>0,ω>0)在区间[0,
]上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )
| π |
| ω |
| A、N=1,M>3 | ||
| B、N=1,M≤3 | ||
C、N=2,M>
| ||
D、N=2,M≤
|
分析:根据曲线的方程可求得函数的周期,进而根据被直线y=4和y=-2所截的弦长相等且不为0,推断出N=
=1,M>
=3.答案可得.
| 4+(-2) |
| 2 |
| 4-(-2) |
| 2 |
解答:解:曲线y=Msin(2ωx+?)+N(M>0,N>0,ω>0)的周期为T=
=
,
被直线y=4和y=-2所截的弦长相等且不为0,
结合图形可得N=
=1,M>
=3.
故选A.
| 2π |
| 2ω |
| π |
| ω |
被直线y=4和y=-2所截的弦长相等且不为0,
结合图形可得N=
| 4+(-2) |
| 2 |
| 4-(-2) |
| 2 |
故选A.
点评:本题主要考查了三角函数图象和性质,对y=Asin(ωx+?)+B(A>0,ω>0),周期为T=
,平衡位置为y=B,ymax=A+B,
ymin=-A+B.
| 2π |
| ω |
ymin=-A+B.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
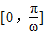 上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )
上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )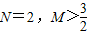
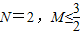
 上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )
上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )

 上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )
上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )
