Question

几何图形是最富于变化的，直角三角形更是如此，但不管怎样变化，其基本图形体现的规律却是相同的，如射影定理的基本图形.这时，从复杂图形中分离出基本图形，就成为解决问题的关键.那么从复杂图形中分离出基本图形有什么窍门呢？你能举例说明吗？

Answer 1

思路:从所给图形中分离出基本图形，利用基本图形写出结论.

探究:在图形的变化中熟悉并掌握射影定理的使用方法，有助于快速发现解题思路.这当中的关键就是把握基本图形，从所给图形中分离出基本图形.如:

(1)在图1-4-4(c)中，求证:CF·CA=CG·CB.

(2)在图1-4-4(a)中，求证:FG·BC=CE·BG.

(3)在图1-4-4(d)中，求证:①CD³=AF·BG·AB；②BC²∶AC²=CF∶FA;

③BC³∶AC³=BG∶AE.就可以这样来思考:

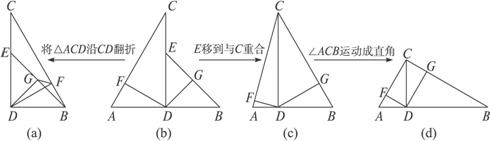
图1-4-4

    在第(1)题中，观察图形则发现分别使用CD²=CF·CA和CD²=CG·CB即可得到证明.

第(2)题可用综合分析法探求解题的思路:欲证FG·BC=CE·BG，只需证，而这四条线段分别属于△BFG和△BEC，能发现这两个三角形存在公共角∠EBC，可选用“两角对应相等”或“两边对应成比例，夹角相等”来证明相似.

或者在图1-4-4(a)中可分解出两个射影定理的基本图形:“Rt△ADE中DG⊥BE”及“Rt△BDC中DF⊥BC”，在两个三角形中分别使用射影定理中的BD²进行代换，得到BG·BE=BF·BC，化成比例式后，可用“两边对应成比例，夹角相等”来证明含有公共角∠EBC的△BFG和△BEC相似.

你可以尝试着自己分析第(3)小题.