题目内容
三棱台是一种重要的多面体,对于图中A1B1C1-ABC,请思考如下问题:

(1)三条侧棱所在的直线一定相交于一点吗?
(2)棱台的侧面是什么样的特殊四边形?
(3)两底面△A1B1C1与△ABC是否具有相似的关系?
若A1B1∶AB=2∶3,求![]() .
.
任意一个棱台的上下底面多边形都是相似多边形吗?(注:这里的两个多边形相似是指它们的对应边分别成比例,对应角分别相等)
(4)若A1B1=AB,则此时的三棱台A1B1C1-ABC可演变成什么样的几何体?
若A1、B1、C1三点收缩为一点(记为P),则此时的三棱台A1B1C1-ABC即P-ABC又演变成了什么样的几何体?
(5)如果几何体A1B1C1-ABC满足△A1B1C1与△ABC相似但不全等,那么这个几何体一定是三棱台吗?
解析:
|
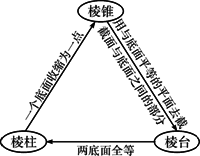
由棱柱、棱锥、棱台的定义,我们可以知道它们之间有如下关系:
又根据定义,棱台与棱锥有很密切的关系,在思考棱台的性质时常常要考虑这一关系.下面我们对以上问题做如下思考: (1)根据定义,棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.所以我们可将三条棱台的侧棱延长得到一个三棱锥,从而三条侧棱所在的直线相交于一点. (2)也是根据定义,棱台的侧面应该是三角形被平行于底边的直线所截后,截线和底线之间的部分,这是一个梯形. (3)由于三棱台两底面对应边互相平行,容易得到它们的对应角相等,所以上下底面是相似的多边形.由相似多边形的知识可知棱台上下底面面积比等于相似比的平方,即 (4)当A1B1=AB,上下底面是全等多边形时,棱台变化成棱柱;当棱台的一个底面缩为一个点时,棱台变为棱锥. (5)我们考虑将三棱柱的上底面旋转一个角度后的情况,此时仍满足上下底面相似但不全等,但形成的图形可能已经不是一个三棱柱了.我们有结论:当不全等的两相似三角形位置摆法不“正”时,不是三棱台. |