题目内容
已知数列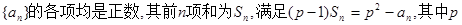 为正常数,且
为正常数,且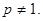
(1)求数列 的通项公式;
的通项公式;
(2)设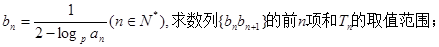
(3)是否存在正整数M,使得 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
【答案】
(1) (2)
(2)
(3)当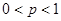 时,存在M=8符合题意
时,存在M=8符合题意
【解析】
试题分析:解:(I)由题设知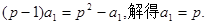 1分
1分
同时
两式作差得
所以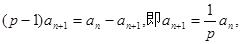
可见,数列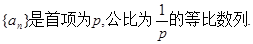 4分
4分
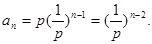 5分
5分
(II) 7分
7分


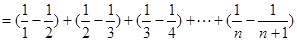
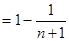 9分
9分
所以,  10分
10分
(III)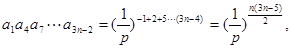
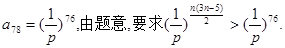 12分
12分
①当
解得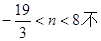 符合题意,此时不存在符合题意的M。 14分
符合题意,此时不存在符合题意的M。 14分
②当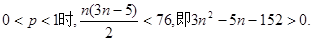
解得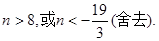 此时存在的符合题意的M=8。
此时存在的符合题意的M=8。
综上所述,当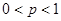 时,存在M=8符合题意 16分
时,存在M=8符合题意 16分
考点:等差数列和等比数列
点评:主要是考查了等差数列A和等比数列的求和与通项公式的综合运用,属于中档题。

练习册系列答案
相关题目