题目内容
已知向量![]() =(x2-3,1),
=(x2-3,1),![]() =(x,-y),(其中实数x和y不同时为零),当|x|<2时,有
=(x,-y),(其中实数x和y不同时为零),当|x|<2时,有![]() ⊥
⊥![]() ,当|x|≥2时,
,当|x|≥2时,![]() ∥
∥![]() .
.
(1)求函数式y=f(x);
(2)求函数f(x)的单调递减区间;
(3)若对![]() x∈(-∞,-2]∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
x∈(-∞,-2]∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
答案:
解析:
解析:
|
解:(1)当 当 得 ∴ (2)当 由 当 ∴函数 (3)对 都有 也就是 对 由(2)知当 ∴函数 又 当 ∴当 综上所述得,对 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
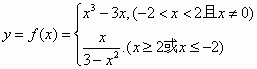 5分
5分 =(3,-2),
=(3,-2), =(x+1,2-x2),则条件“x=2”是条件“a∥b”成立的
=(x+1,2-x2),则条件“x=2”是条件“a∥b”成立的 =(x1,y1),
=(x1,y1), =(x2,y2),若|
=(x2,y2),若| 的值为
( )
的值为
( ) B.
B. C.
C.  D.
D.