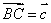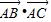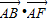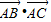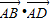题目内容
如图,在边长为1的正方体ABCD-A1B1C1D1中,E为AD中点,(1)求二面角E-A1C1-D1的平面角的余弦值;
(2)求四面体B-A1C1E的体积.
(3)(文) 求E点到平面A1C1B的距离
(4)(文)求二面角B-A1C1-B1的平面角的余弦值.

【答案】分析:(1)先作出二面角E-A1C1-D1的平面角:在A1D1上取中点F.连接EF过F作FM⊥A1C1于A1C1上一点M,连接EM,则∠EMF为二面角E-A1C1-D1的平面角.再在△A1C1D1中,可求;
(2)求四面体B-A1C1E的体积,可以转换底面,求VC1-A1BN,即可;
(3)将E到平面BA1C1的距离转化为M点到平面BA1C1的距离,再在△MHB中可求;
(4)先利用三垂线定理确定二面角的平面角,再在△BO1B1中求解.
解答:解:(1)在边长为1的正方体ABCD-A1B1C1D1,E为AD中点,在A1D1上取中点F.连接EF过F作FM⊥A1C1于A1C1上一点M,连接EM,则∠EMF为二面角E-A1C1-D1的平面角.
在△A1C1D1中,FM= B1D1=
B1D1=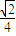 ,又EF⊥FM,EF=1
,又EF⊥FM,EF=1
∴tan∠EMF=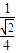 =2
=2 ,从而cos∠EMF=
,从而cos∠EMF= .
.
∴二面角E-A1C1-D1的余弦值为
(2)在平面ABCD内,延长BA到N点,使AN= ,故NE∥A1C1,∴NE∥面BA1C1
,故NE∥A1C1,∴NE∥面BA1C1
∴VB-A1C1E=VE-A1BC1=VN-A1C1E=VC1-A1BN
= •(
•( •
• •1)•1=
•1)•1=

(3)(文)取DC中点F,连接EF交BD于M点,又E为AD中点,故可知EF∥A1C1,则EF∥面BA1C1,
因此E到平面BA1C1的距离就是M点到平面BA1C1的距离.
在对角面BA1D1D内,过M作MH⊥O1B交OB1于H,
∵A1C1⊥面BB1D1D,则面BD1⊥面BA1C1而MH⊥O1B,则MH⊥面BA1C1,
又∵sin∠DBO1=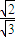 故在△MHB中,MH=BM•sin∠DBO1=
故在△MHB中,MH=BM•sin∠DBO1=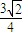 •
• =
=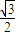
故E到平面BA1C1之距离为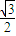
(4)

在边长为1的正方体ABCD-A1B1C1D1连B1D1,则B1D1⊥A1C1,设其交点为O1,连O1B.
则由三垂线定理可知O1B⊥A1C1
∴∠BO1B1为二面角B-A1C1-B1的平面角.
又BB1=1,O1B= ,∴tan∠BO1B1=
,∴tan∠BO1B1= ,从而cos∠BO1B1=
,从而cos∠BO1B1=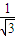 =
= .
.
点评:本题的考点是与二面角有关的立体几何综合问题,主要考查二面角的求法,考查几何体的体积,关键是作(找)二面角的平面角.
(2)求四面体B-A1C1E的体积,可以转换底面,求VC1-A1BN,即可;
(3)将E到平面BA1C1的距离转化为M点到平面BA1C1的距离,再在△MHB中可求;
(4)先利用三垂线定理确定二面角的平面角,再在△BO1B1中求解.
解答:解:(1)在边长为1的正方体ABCD-A1B1C1D1,E为AD中点,在A1D1上取中点F.连接EF过F作FM⊥A1C1于A1C1上一点M,连接EM,则∠EMF为二面角E-A1C1-D1的平面角.
在△A1C1D1中,FM=
 B1D1=
B1D1=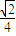 ,又EF⊥FM,EF=1
,又EF⊥FM,EF=1∴tan∠EMF=
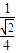 =2
=2 ,从而cos∠EMF=
,从而cos∠EMF= .
.∴二面角E-A1C1-D1的余弦值为

(2)在平面ABCD内,延长BA到N点,使AN=
 ,故NE∥A1C1,∴NE∥面BA1C1
,故NE∥A1C1,∴NE∥面BA1C1∴VB-A1C1E=VE-A1BC1=VN-A1C1E=VC1-A1BN
=
 •(
•( •
• •1)•1=
•1)•1=

(3)(文)取DC中点F,连接EF交BD于M点,又E为AD中点,故可知EF∥A1C1,则EF∥面BA1C1,
因此E到平面BA1C1的距离就是M点到平面BA1C1的距离.
在对角面BA1D1D内,过M作MH⊥O1B交OB1于H,
∵A1C1⊥面BB1D1D,则面BD1⊥面BA1C1而MH⊥O1B,则MH⊥面BA1C1,
又∵sin∠DBO1=
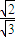 故在△MHB中,MH=BM•sin∠DBO1=
故在△MHB中,MH=BM•sin∠DBO1=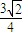 •
• =
=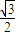
故E到平面BA1C1之距离为
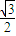
(4)

在边长为1的正方体ABCD-A1B1C1D1连B1D1,则B1D1⊥A1C1,设其交点为O1,连O1B.
则由三垂线定理可知O1B⊥A1C1
∴∠BO1B1为二面角B-A1C1-B1的平面角.
又BB1=1,O1B=
 ,∴tan∠BO1B1=
,∴tan∠BO1B1= ,从而cos∠BO1B1=
,从而cos∠BO1B1=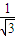 =
= .
.点评:本题的考点是与二面角有关的立体几何综合问题,主要考查二面角的求法,考查几何体的体积,关键是作(找)二面角的平面角.

练习册系列答案
相关题目
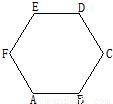
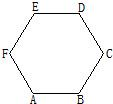
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|