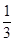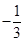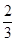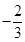题目内容
已知向量a=(3sin α,cos α),b=(2sin α,5sin α-4cos α),α∈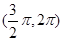 ,且a⊥b.
,且a⊥b.
(1)求tan α的值;
(2)求cos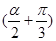 的值.
的值.
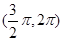 ,且a⊥b.
,且a⊥b.(1)求tan α的值;
(2)求cos
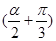 的值.
的值.(1)-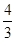 (2)
(2)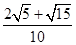
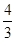 (2)
(2)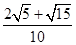
(1)∵a⊥b,∴a·b=0.
而a=(3sin α,cos α),b=(2sin α,5sin α-4cos α),
故a·b=6sin2α+5sin αcos α-4cos2α=0,
即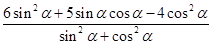 =0.
=0.
由于cos α≠0,∴6tan2α+5tan α-4=0.
解得tan α=-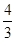 或tan α=
或tan α=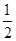 .
.
∵α∈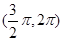 ,∴tan α<0,
,∴tan α<0,
∴tan α=-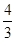 .
.
(2)∵α∈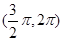 ,∴
,∴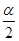 ∈
∈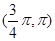 .
.
由tan α=-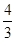 ,求得tan
,求得tan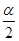 =-
=-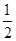 或tan
或tan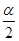 =2(舍去).
=2(舍去).
∴sin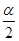 =
=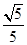 ,cos
,cos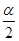 =-
=-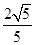 ,
,
∴cos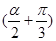 =cos
=cos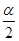 cos
cos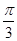 -sin
-sin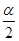 ·sin
·sin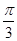 =-
=-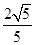 ×
×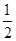 -
-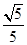 ×
×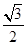 =-
=-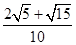
而a=(3sin α,cos α),b=(2sin α,5sin α-4cos α),
故a·b=6sin2α+5sin αcos α-4cos2α=0,
即
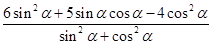 =0.
=0.由于cos α≠0,∴6tan2α+5tan α-4=0.
解得tan α=-
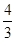 或tan α=
或tan α=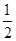 .
.∵α∈
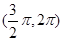 ,∴tan α<0,
,∴tan α<0,∴tan α=-
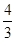 .
.(2)∵α∈
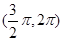 ,∴
,∴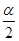 ∈
∈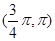 .
.由tan α=-
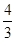 ,求得tan
,求得tan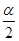 =-
=-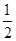 或tan
或tan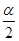 =2(舍去).
=2(舍去).∴sin
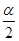 =
=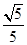 ,cos
,cos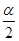 =-
=-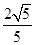 ,
,∴cos
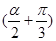 =cos
=cos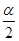 cos
cos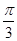 -sin
-sin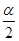 ·sin
·sin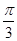 =-
=-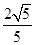 ×
×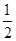 -
-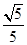 ×
×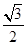 =-
=-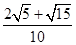

练习册系列答案
相关题目
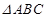 中,角
中,角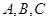 所对的边为
所对的边为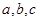 ,角
,角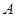 为锐角,若
为锐角,若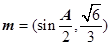 ,
,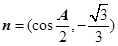 且
且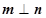 .
.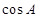 的大小;
的大小;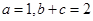 ,求
,求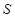 .
. ,角α是第二象限角,则tan(2π-α)等于( )
,角α是第二象限角,则tan(2π-α)等于( )

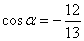 ,
, ,则
,则 的值是 .
的值是 .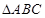 中,
中,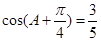 ,则
,则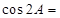 .
. ,则
,则 =______________.
=______________.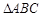 中,若
中,若 ,则
,则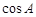 =( )
=( )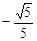
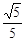
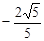
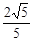
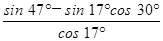 的值是( ).
的值是( ). 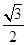
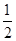
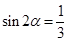 ,则
,则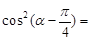 ( )
( )