题目内容
体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p (p≠0),发球次数为X,若X的数学期望EX>1.75,则p的取值范围是( )
A、(0,
| ||
B、(
| ||
C、(0,
| ||
D、(
|
分析:根据题意,首先求出X=1、2、3时的概率,进而可得EX的表达式,由题意EX>1.75,可得p2-3p+3>1.75,解可得p的范围,结合p的实际意义,对求得的范围可得答案.
解答:解:根据题意,学生一次发球成功的概率为p,即P(X=1)=p,
二次发球成功的概率P(X=2)=p(1-p),
三次发球成功的概率P(X=3)=p(1-p)2,
则Ex=p+2p(1-p)+3p(1-p)2=p2-3p+3,
依题意有EX>1.75,则p2-3p+3>1.75,
解可得,p>
或p<
,
结合p的实际意义,可得0<p<
,即p∈(0,
)
故选C.
二次发球成功的概率P(X=2)=p(1-p),
三次发球成功的概率P(X=3)=p(1-p)2,
则Ex=p+2p(1-p)+3p(1-p)2=p2-3p+3,
依题意有EX>1.75,则p2-3p+3>1.75,
解可得,p>
| 5 |
| 2 |
| 1 |
| 2 |
结合p的实际意义,可得0<p<
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查期望的计算,注意解题的最后要结合概率的意义对求出的答案范围进行取舍.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
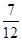 ) B. (
) B. ( ) D. (
) D. ( )
) ,1)
,1) )
) ,1)
,1)