题目内容
若一个圆锥轴截面(过圆锥顶点和底面直径的截面)是面积为
的等边三角形则这个圆锥的全面积为( )
| 3 |
分析:设圆锥的底面半径为r、高为h、母线为l,由等边三角形的性质与三角形的面积公式,建立方程组解出r=1,h=
且l=2.再根据圆锥的侧面积公式与圆的面积公式加以计算,可得此圆锥的全面积.
| 3 |
解答:解: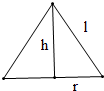 设圆锥的底面半径为r、高为h、母线为l,
设圆锥的底面半径为r、高为h、母线为l,
∵圆锥轴截面是面积为
的等边三角形,
∴l=2r且S=
×r×h=
,
解得r=1,h=
且l=2.
因此这个圆锥的全面积为
S=S底+S侧=πr2+πrl=π×12+π×1×2=3π.
故选:A
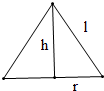 设圆锥的底面半径为r、高为h、母线为l,
设圆锥的底面半径为r、高为h、母线为l,∵圆锥轴截面是面积为
| 3 |
∴l=2r且S=
| 1 |
| 2 |
| 3 |
解得r=1,h=
| 3 |
因此这个圆锥的全面积为
S=S底+S侧=πr2+πrl=π×12+π×1×2=3π.
故选:A
点评:本题给出圆锥的轴截面的形状,求圆锥的全面积.着重考查了等边三角形的性质、圆锥的侧面积公式等知识,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目