题目内容
已知数列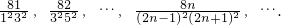 Sn为其前n项和.计算得
Sn为其前n项和.计算得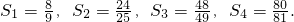 观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.
观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.
解:观察分析题设条件可知
证明如下:(1)当n=1时,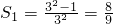 ,等式成立.
,等式成立.
(Ⅱ)设当n=k时等式成立,即 则
则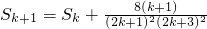 =
= =
=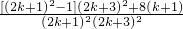 =
= =
= =
= =
=
由此可知,当n=k+1时等式也成立.根据(1)(2)可知,等式对任何n∈N都成立
分析:观察分析题设条件可知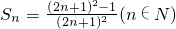 .然后再用数学归纳法进行证明.
.然后再用数学归纳法进行证明.
点评:本题考查数列性质的综合应用,解题时要注意数学归纳法的证明步骤,注意培养计算能力.

证明如下:(1)当n=1时,
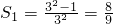 ,等式成立.
,等式成立.(Ⅱ)设当n=k时等式成立,即
 则
则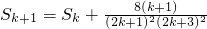 =
= =
=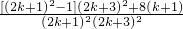 =
= =
= =
= =
=
由此可知,当n=k+1时等式也成立.根据(1)(2)可知,等式对任何n∈N都成立
分析:观察分析题设条件可知
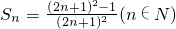 .然后再用数学归纳法进行证明.
.然后再用数学归纳法进行证明.点评:本题考查数列性质的综合应用,解题时要注意数学归纳法的证明步骤,注意培养计算能力.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
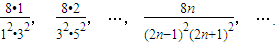 Sn为其前n项和.计算得
Sn为其前n项和.计算得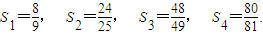 观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.
观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.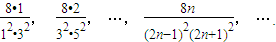 Sn为其前n项和.计算得
Sn为其前n项和.计算得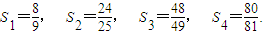 观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.
观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明.