题目内容
正弦曲线y=sinx与余弦曲线y=cosx及直线x=0和直线x=  所围成区域的面积为 。
所围成区域的面积为 。
 所围成区域的面积为 。
所围成区域的面积为 。
试题分析:根据正弦曲线y=sinx与余弦曲线y=cosx在x=
 处有交点(
处有交点( ,
, ),将所求面积分为两部分
),将所求面积分为两部分
函数y=cosx-sinx在[0,
 ]上的积分值与函数y=sinx-cosx在[
]上的积分值与函数y=sinx-cosx在[ ,π]上的积分值之和,再根据定积分计算公式,即可得到所求的面积。
,π]上的积分值之和,再根据定积分计算公式,即可得到所求的面积。
点评:本题给出正、余弦曲线,求它们被直线x=0和直线x=π所围成区域的面积,着重考查了定积分的几何意义和积分计算公式等知识点,属于基础题.

练习册系列答案
相关题目
 ),其中ω>0,|
),其中ω>0,| ,若cos
,若cos cos
cos sin
sin .
. .
. 的最小正周期及其单调增区间:
的最小正周期及其单调增区间: 时,求
时,求 的结果是( )
的结果是( )



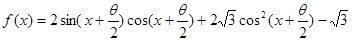
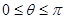 ,求
,求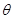 使函数
使函数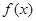 为偶函数。
为偶函数。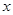 ∈[-π,π]的
∈[-π,π]的
 ,则
,则
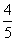



 -2x)的单调增区间是[
-2x)的单调增区间是[ ],kÎZ
],kÎZ
 sin(wx)的最小正周期为4p,则w=
sin(wx)的最小正周期为4p,则w=