题目内容
完成下列填空,并按要求画出函数的简图,不写画法,请保留画图过程中的痕迹,痕迹用虚线表示,最后成图部分用实线表示.
(1)函数y=|x2-2x-3|的零点是________,利用函数y=x2-2x-3的图象,在直角坐标系(1)中画出函数y=|x2-2x-3|的图象.
(2)函数y=2|x|+1的定义域是________,值域是________,是________函数(填“奇”、“偶”或“非奇非偶”).利用y=2x的图象,通过适当的变换,在直角坐标系(2)中画出函数y=2|x|+1的图象.
解:(1)令|x2-2x-3|=0,解得x=-1或3
故答案为:-1,3
图象如下图:
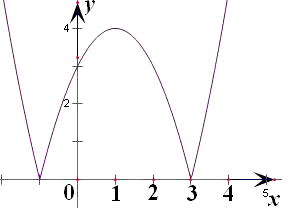
(2)函数y=2|x|+1的定义域是R,∵|x|≥0,∴2|x|≥1
∴2|x|+1≥2即函数y=2|x|+1的值域为[2,+∞)
f(-x)=2|-x|+1=2|x|+1=f(x)
∴函数y=2|x|+1为偶函数
故答案为:R,[2,+∞),偶
函数y=2|x|+1的图象如下图
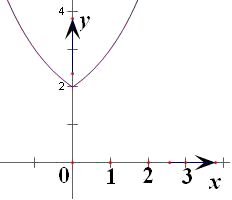
分析:(1)令|x2-2x-3|=0,可求出函数的零点,然后画出函数y=x2-2x-3的图象,将x轴下方的图象翻折到x轴上方即可;
(2)函数y=2|x|+1的定义域为R,求出|x|的范围,然后根据指数函数的性质可求出值域,根据奇偶性的定义可的该函数的奇偶性,然后根据图象变换画出图形即可.
点评:本题主要考查了函数的定义域,值域,奇偶性以及零点等有关指数,同时考查了图象变换以及作图能力,属于中档题.
故答案为:-1,3
图象如下图:

(2)函数y=2|x|+1的定义域是R,∵|x|≥0,∴2|x|≥1
∴2|x|+1≥2即函数y=2|x|+1的值域为[2,+∞)
f(-x)=2|-x|+1=2|x|+1=f(x)
∴函数y=2|x|+1为偶函数
故答案为:R,[2,+∞),偶
函数y=2|x|+1的图象如下图

分析:(1)令|x2-2x-3|=0,可求出函数的零点,然后画出函数y=x2-2x-3的图象,将x轴下方的图象翻折到x轴上方即可;
(2)函数y=2|x|+1的定义域为R,求出|x|的范围,然后根据指数函数的性质可求出值域,根据奇偶性的定义可的该函数的奇偶性,然后根据图象变换画出图形即可.
点评:本题主要考查了函数的定义域,值域,奇偶性以及零点等有关指数,同时考查了图象变换以及作图能力,属于中档题.

练习册系列答案
相关题目