Question

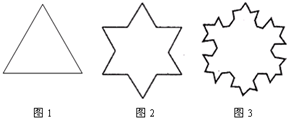一艘太空飞船飞往地球，第一次观测时，如图1发现一个正三角形的岛屿（边长为

3

）；第二次观测时，如图2发现它每边中央

1

3

处还有一正三角形海岬，形成了六角的星形；第三次观测时，如图3发现原先每一小边的中央

1

3

处又有一向外突出的正三角形海岬，把这个过程无限地继续下去，就得到著名的数学模型--柯克岛．把第1，2，3，…，n次观测到的岛的海岸线长记为a₁，a₂，a₃，…，a_n，试求a₁，a₂，a₃的值及a_n的表达式．

Answer 1

分析：因为第一个图形的边长为

3

，从第二个图形起，每一个图形的边长均为上一个图形边长的

1

3

，利用等比数列的通项公式即可得出第n个图形的边长；因为第一个图形的边数为3，从第二个图形起，每一个图形的边数均为上一个图形边数的4倍，利用等比数列的通项公式即可得出．

解答：解：由题意知，a1=3

3

，  a2=3

3

×

4

3

=4

3

，  a3=3

3

×(

4

3

)2=

16

3

3

．
因为第一个图形的边长为

3

，从第二个图形起，每一个图形的边长均为上一个图形边长的

1

3

，所以第n个图形的边长为

3

•(

1

3

)n-1；                        
因为第一个图形的边数为3，从第二个图形起，每一个图形的边数均为上一个图形边数的4倍，所以第n个图形的边数为3×4^n-1．
因此，an=3

3

•(

4

3

)n-1．

点评：正确找出规律和熟练掌握等比数列的通项公式是解题的关键．