题目内容
某同学在研究函数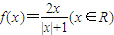 时,分别得出如下几个结论:
时,分别得出如下几个结论:①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(-2,2);
③若x1≠x2,则一定有f(x1)≠f(x2);
④函数y(x)=f(x)-2x在R上有三个零点.
其中正确的序号有 .
【答案】分析:由奇偶性的定义来判断①,由分类讨论结合反比例函数的单调性求解②;由②结合①对称区间上的单调性相同说明③正确;由数形结合来说明④不正确.
解答:解:①f(-x)=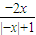 =-f(x)∴正确
=-f(x)∴正确
②当x>0时,f(x)=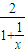 ∈(0,2)
∈(0,2)
由①知当x<0时,f(x)∈(-2,0)
x=0时,f(x)=0
∴f(x)∈(-2,2)正确;
③则当x>0时,f(x)= 反比例函数的单调性可知,f(x)在(0,+∞)上是增函数
反比例函数的单调性可知,f(x)在(0,+∞)上是增函数
再由①知f(x)在(-∞,0)上也是增函数,正确
④由③知f(x)的图象与y=2x只有两个交点.不正确.
故答案为:①②③
点评:本题主要考查了函数的定义域,单调性,奇偶性,值域,考查全面,方法灵活,这四个问题在研究时往往是同时考虑,属于基础题.
解答:解:①f(-x)=
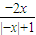 =-f(x)∴正确
=-f(x)∴正确②当x>0时,f(x)=
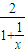 ∈(0,2)
∈(0,2)由①知当x<0时,f(x)∈(-2,0)
x=0时,f(x)=0
∴f(x)∈(-2,2)正确;
③则当x>0时,f(x)=
 反比例函数的单调性可知,f(x)在(0,+∞)上是增函数
反比例函数的单调性可知,f(x)在(0,+∞)上是增函数再由①知f(x)在(-∞,0)上也是增函数,正确
④由③知f(x)的图象与y=2x只有两个交点.不正确.
故答案为:①②③
点评:本题主要考查了函数的定义域,单调性,奇偶性,值域,考查全面,方法灵活,这四个问题在研究时往往是同时考虑,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
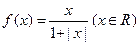 时,分别给出下面几个结论:
时,分别给出下面几个结论: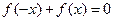 对
对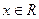 恒成立;
恒成立; 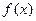 的值域为
的值域为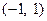 ;
;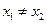 ,则一定有
,则一定有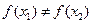 ;
;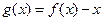 在
在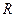 上有三个零点.
上有三个零点.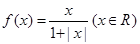 时,分别给出下面几个结论:
时,分别给出下面几个结论: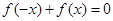 对
对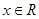 恒成立; ②函数
恒成立; ②函数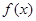 的值域为
的值域为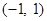 ;
;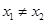 ,则一定有
,则一定有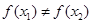 ; ④函数
; ④函数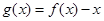 在
在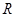 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.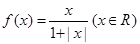 时,分别给出下面几个结论:
时,分别给出下面几个结论: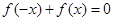 对
对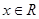 恒成立; ②函数
恒成立; ②函数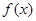 的值域为
的值域为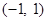 ;
;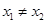 ,则一定有
,则一定有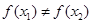 ; ④函数
; ④函数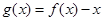 在
在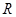 上有三个零点。
上有三个零点。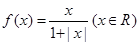 时,分别给出下面几个结论:
时,分别给出下面几个结论: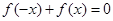 对
对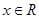 恒成立;
恒成立; 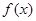 的值域为
的值域为 ;
;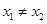 ,则一定有
,则一定有 ;
; 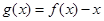 在
在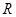 上有三个零点.
上有三个零点.