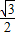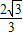Question

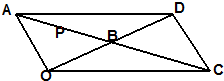在点O处测得远处质点P作匀速直线运动，开始位置在A点，一分钟后到达B点，再过一分钟到达C点，测得∠AOB=90°，∠BOC=30°，则tan∠OAB=（　　）

• A．

  3

  2

• B．

  3

  2

• C．

  2 3

  3

• D．

  2

  3

Answer 1

分析：做出辅助线延长OB到D，使得BD=OB，得到四边形OADC为平行四边形，得到∠ODC=∠AOB=90°，利用直角三角形中三角函数的定义求出结果．

解答：解：如图延长OB到D，使得BD=OB，
则四边形OADC为平行四边形
∴∠ODC=∠AOB=90°，
又∠BOC=30°，
则OB=

1

2

OD=

3

2

DC=

3

2

OA，
tan∠OAB=

OB

OA

=

3

2

，
故选B．

点评：本题考查三角函数的定义，本题解题的关键是根据所给的条件看出要用的线段之间的关系，本题是一个基础题．