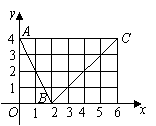
题目内容
(08年北京卷理)(本小题共14分)
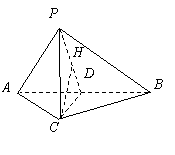
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
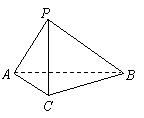
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【标准答案】: 解法一:
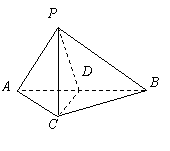
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
, ![]() .
.
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
, ![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
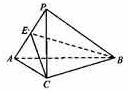
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 的长即为点
的长即为点![]() 到平面
到平面![]() 的距离.
的距离.
由(Ⅰ)知![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:
(Ⅰ)![]() ,
,![]() ,
, ![]() .
.
又![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)如图,
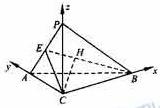
以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
,![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() ,
,
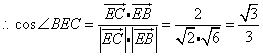 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)![]() ,
,
![]() 在平面
在平面![]() 内的射影为正
内的射影为正![]() 的中心
的中心![]() ,且
,且![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系![]() .
.
![]() ,
, ![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
【高考考点】: 直线与直线的垂直,二面角,点面距离
【易错提醒】: 二面角的平面角找不到,求点面距离的方法单一
【备考提示】: 找二面角的方法大致有十种左右,常见的也有五六种,希望能够全面掌握。

练习册系列答案
相关题目