题目内容
若△ABC中,sinA:sinB:sinC=2:3:4,那么cosC=( )A.
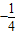
B.

C.
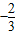
D.

【答案】分析:通过正弦定理求出,a:b:c=2:3:4,设出a,b,c,利用余弦定理直接求出cosC即可.
解答:解:因为sinA:sinB:sinC=2:3:4
所以a:b:c=2:3:4,设a=2k,b=3k,c=4k
由余弦定理可知:
cosC=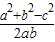 =
=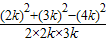 =-
=- .
.
故选A.
点评:本题是基础题,考查正弦定理与余弦定理的应用,考查计算能力.
解答:解:因为sinA:sinB:sinC=2:3:4
所以a:b:c=2:3:4,设a=2k,b=3k,c=4k
由余弦定理可知:
cosC=
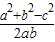 =
=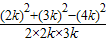 =-
=- .
.故选A.
点评:本题是基础题,考查正弦定理与余弦定理的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =(1+cosα,sinα),
=(1+cosα,sinα), =(1-cosβ,sinβ),
=(1-cosβ,sinβ), ,α∈(0,π),β∈(π,2π),向量
,α∈(0,π),β∈(π,2π),向量 与
与 夹角为θ1,向量
夹角为θ1,向量 与
与 夹角为θ2,且θ1-θ2=
夹角为θ2,且θ1-θ2= ,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.
,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α. ,试求b+c取值范围.
,试求b+c取值范围. =(1+cosα,sinα),
=(1+cosα,sinα), =(1-cosβ,sinβ),
=(1-cosβ,sinβ), ,α∈(0,π),β∈(π,2π),向量
,α∈(0,π),β∈(π,2π),向量 与
与 夹角为θ1,向量
夹角为θ1,向量 与
与 夹角为θ2,且θ1-θ2=
夹角为θ2,且θ1-θ2= ,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.
,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.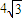 ,试求b+c取值范围.
,试求b+c取值范围. =(1+cosα,sinα),
=(1+cosα,sinα), =(1-cosβ,sinβ),
=(1-cosβ,sinβ), ,α∈(0,π),β∈(π,2π),向量
,α∈(0,π),β∈(π,2π),向量 与
与 夹角为θ1,向量
夹角为θ1,向量 与
与 夹角为θ2,且θ1-θ2=
夹角为θ2,且θ1-θ2=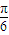 ,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.
,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.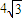 ,试求b+c取值范围.
,试求b+c取值范围.