题目内容
下列不等式的证明明过程：①若a，b∈R，则
| b |
| a |
| a |
| b |
|
| xy |
③若x∈R，则|x+
| 4 |
| x |
| 4 |
| |x| |
|x|•
|
④若a，b∈R，ab＜0，则
| b |
| a |
| a |
| b |
| -b |
| a |
| -a |
| b |
|
其中正确的序号是
分析：依次分析4个命题：a＜0，b＞0时，
+
＜0，故①不正确．当x=
，y=
时，检验②不正确，利用基本不等式可得③④正确，综合可得答案．
| b |
| a |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：当a，b∈R且 a＜0，b＞0时，
+
＜0，故①不正确．
当x=
，y=
时，lgx 和lgy 都等于-lg2，小于0，故②不正确．
∵|x+
|=|x|+|
|≥2
=4，故③正确．
若a，b∈R，ab＜0，则
+
=-(
+
)≤-2
=-2，故④正确．
故答案为 ③、④．
| b |
| a |
| a |
| b |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
∵|x+
| 4 |
| x |
| 4 |
| x |
|x|•|
|
若a，b∈R，ab＜0，则
| b |
| a |
| a |
| b |
| -b |
| a |
| -a |
| b |
|
故答案为 ③、④．
点评：本题考查不等式性质的应用，基本不等式的应用，注意考虑特殊情况和基本不等式的使用条件，属于中档题．
练习册系列答案
相关题目
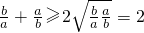②若x，y∈R，则
；
；
．
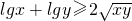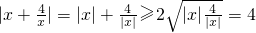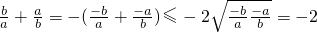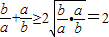②若x，y∈R，则
；
；
．
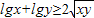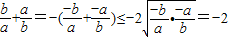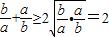②若x，y∈R，则
；
；
．
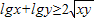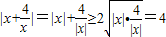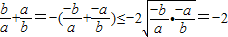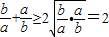②若x，y∈R，则
；
；
．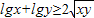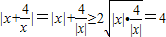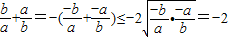