题目内容
已知过点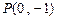 的直线
的直线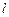 与抛物线
与抛物线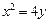 相交于
相交于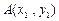 、
、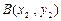 两点,
两点,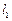 、
、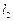 分别是该抛物线在
分别是该抛物线在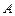 、
、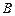 两点处的切线,
两点处的切线,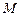 、
、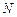 分别是
分别是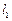 、
、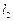 与直线
与直线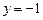 的交点.
的交点.
(1)求直线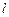 的斜率的取值范围;
的斜率的取值范围;
(2)试比较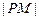 与
与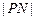 的大小,并说明理由.
的大小,并说明理由.
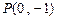 的直线
的直线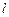 与抛物线
与抛物线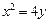 相交于
相交于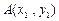 、
、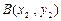 两点,
两点,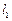 、
、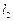 分别是该抛物线在
分别是该抛物线在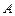 、
、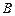 两点处的切线,
两点处的切线,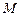 、
、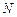 分别是
分别是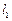 、
、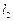 与直线
与直线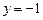 的交点.
的交点.(1)求直线
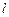 的斜率的取值范围;
的斜率的取值范围;(2)试比较
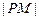 与
与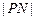 的大小,并说明理由.
的大小,并说明理由. (1)直线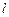 的斜率的取值范围:k<﹣1 或 k >1;(2)
的斜率的取值范围:k<﹣1 或 k >1;(2)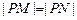 .
.
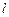 的斜率的取值范围:k<﹣1 或 k >1;(2)
的斜率的取值范围:k<﹣1 或 k >1;(2)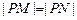 .
.1)设直线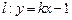 ,则
,则
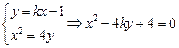 ,
,
依题意,有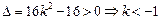 或
或 ;
;
(2)由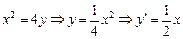 ,所以抛物线在
,所以抛物线在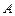 处的切线
处的切线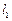 的方程为
的方程为
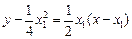 ,即
,即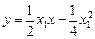 .
.
令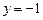 ,得
,得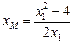 .
.
同理,得 .
.
注意到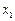 、
、 是方程①的两个实根,故
是方程①的两个实根,故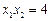 ,即
,即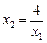 ,从而有
,从而有
 ,
,
因此,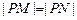 .
.
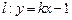 ,则
,则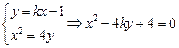 ,
, 依题意,有
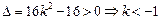 或
或 ;
;(2)由
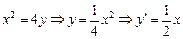 ,所以抛物线在
,所以抛物线在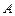 处的切线
处的切线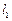 的方程为
的方程为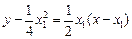 ,即
,即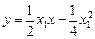 .
.令
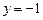 ,得
,得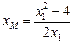 .
.同理,得
 .
.注意到
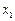 、
、 是方程①的两个实根,故
是方程①的两个实根,故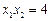 ,即
,即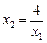 ,从而有
,从而有 ,
,因此,
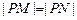 .
.
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
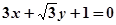 的倾斜角是( )
的倾斜角是( )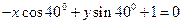 的倾斜角是( )
的倾斜角是( )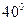

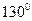
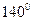
 上至少有三个不同点到直线
上至少有三个不同点到直线 的距离为
的距离为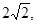 则直线
则直线 的斜率的取值区间为 .
的斜率的取值区间为 .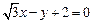 的倾斜角为 ▲
的倾斜角为 ▲  的倾斜角大小为___ __(用反三角形式表示).
的倾斜角大小为___ __(用反三角形式表示). 经过点
经过点 (
( ,1),
,1), (-3,4),
(-3,4), 经过点
经过点 (1,
(1, (-1,
(-1, ),当直线
),当直线