题目内容
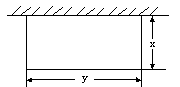
某中学为美化校园,拟用篱笆围一个矩形花圃,其面积为200m2,该矩形花圃的一边利用学校旧围墙(足够长),如图所示,设矩形的一边为xm,另一边为ym。
(Ⅰ)求出y与x的函数关系式,并写出其定义域;
(Ⅱ)当x为何值时,所用篱笆最短,最短的篱笆是多少?
(Ⅰ)求出y与x的函数关系式,并写出其定义域;
(Ⅱ)当x为何值时,所用篱笆最短,最短的篱笆是多少?
解:(Ⅰ)依题意,矩形面积为200m2,
即xy=200,
∴y与x的函数关系式是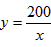 ,定义域是(0,+∞);
,定义域是(0,+∞);
(Ⅱ)篱笆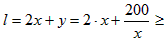 2
2 ,
,
当且仅当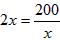 ,即x=10时,等号成立,
,即x=10时,等号成立,
∴当x=10时,lmin=40,
答:当x为10m时,所用篱笆最短,最短的篱笆是40m。
即xy=200,
∴y与x的函数关系式是
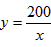 ,定义域是(0,+∞);
,定义域是(0,+∞);(Ⅱ)篱笆
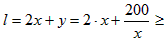 2
2 ,
,当且仅当
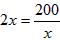 ,即x=10时,等号成立,
,即x=10时,等号成立, ∴当x=10时,lmin=40,
答:当x为10m时,所用篱笆最短,最短的篱笆是40m。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目